Understanding the Formulation of Hypothesis and Research Problem Definition
Research problems arise from situations requiring solutions, faced by individuals, groups, organizations, or society. Researchers define research problems through questions or issues they aim to answer or solve. Various sources such as intuitions, research studies, brainstorming sessions, and consul
5 views • 25 slides
Boyfriend Girlfriend Love Relationship Problems Solution
In Islamic astrology, the celestial bodies\u2019 positions and movements are believed to influence human affairs, including relationships, Boyfriend Girlfriend Love Relationship Problems Solution also. Islamic astrology combines principles of traditional astrology with Islamic teachings and beliefs.
2 views • 3 slides
Understanding The Simplex Method for Linear Programming
The simplex method is an algebraic procedure used to solve linear programming problems by maximizing or minimizing an objective function subject to certain constraints. This method is essential for dealing with real-life problems involving multiple variables and finding optimal solutions. The proces
0 views • 56 slides
Linear Programming Models for Product-Mix Problems and LP Problem Solutions
This unit covers the formulation of linear programming (LP) models for product-mix problems, including graphical and simplex methods for solving LP problems along with the concept of duality. It also delves into transportation problems, offering insights into LP problem resolution techniques.
0 views • 137 slides
Understanding Complexity in Polynomial Time: MAJORITY-3SAT and Related Problems
Dive into the world of MAJORITY-3SAT and its related problems, exploring the complexity of CNF formulas and the satisfiability of assignments. Discover the intricacies of solving canonical NP-complete problems and the significance of variables in determining computational complexity.
3 views • 35 slides
Learning Objectives in Mathematics Education
The learning objectives in this mathematics course include identifying key words, translating sentences into mathematical equations, and developing problem-solving strategies. Students will solve word problems involving relationships between numbers, geometric problems with perimeter, percentage and
0 views • 30 slides
Introduction to Mathematical Programming and Optimization Problems
In optimization problems, one aims to maximize or minimize an objective based on input variables subject to constraints. This involves mathematical programming where functions and relationships define the objective and constraints. Linear, integer, and quadratic programs represent different types of
0 views • 25 slides
Examples of Optimization Problems Solved Using LINGO Software
This content provides examples of optimization problems solved using LINGO software. It includes problems such as job assignments to machines, finding optimal solutions, and solving knapsack problems. Detailed models, constraints, and solutions are illustrated with images. Optimization techniques an
1 views • 41 slides
Formulation of Linear Programming Problems in Decision Making
Linear Programming is a mathematical technique used to optimize resource allocation and achieve specific objectives in decision-making. The nature of Linear Programming problems includes product-mix and blending problems, with components like decision variables and constraints. Various terminologies
1 views • 14 slides
Understanding Optimization Techniques for Design Problems
Explore the basic components of optimization problems, such as objective functions, constraints, and global vs. local optima. Learn about single vs. multiple objective functions and constrained vs. unconstrained optimization problems. Dive into the statement of optimization problems and the concept
0 views • 96 slides
RESOLUTION METHOD IN AI
Resolution method in AI is an inference rule used in propositional and first-order predicate logic to prove sentence satisfiability. It employs a proof by refutation technique to achieve contradiction, ultimately concluding the original goal's truth. The process involves converting statements to cla
0 views • 12 slides
Satisfiability Modulo Abstraction for Separation Logic with Linked Lists
This study explores the application of satisfiability modulo abstraction in separation logic with linked lists. It presents a technique using abstract interpretation concepts to handle separation logic formulas beyond previous methods, specifically focusing on over-approximating heaps that satisfy t
0 views • 41 slides
Engaging Mathematics Problems for Critical Thinking and Fun Learning
Explore a collection of engaging mathematics problems and classical brain teasers that challenge students to think critically, problem-solve creatively, and have fun while learning. From dissection tasks to card dealing challenges, these problems encourage students to readjust, reformulate, and exte
0 views • 36 slides
Algorithm Design Techniques: Divide and Conquer
Algorithm design techniques such as divide and conquer, dynamic programming, and greedy algorithms are essential for solving complex problems by breaking them down into smaller sub-problems and combining their solutions. Divide and conquer involves breaking a problem into unrelated sub-problems, sol
1 views • 13 slides
Understanding Satisfiability Modulo Theories: Lecture Insights
Variables, terms, signatures, and formulas explained in first-order logic. Explore models, interpretations, and satisfiability modulo theories (SMT). Discover common theories like EUF, LIA, LRA, and decision procedures for EUF.
0 views • 21 slides
Understanding and Treating Sleep Problems in Children with Autism
Sleep problems in children with autism are viewed as skill deficits that can be addressed through relevant skills teaching. Good sleep is crucial for children's overall well-being, as it affects mood, behavior, learning, and physical health. Lack of good sleep can lead to irritability, fatigue, unin
0 views • 75 slides
Computational Complexity and NP-Complete Problems
In today's discussion, we delved into computational complexity and the challenges faced in finding efficient algorithms for various problems. We explored how some problems defy easy categorization and resist polynomial-time solutions. The concept of NP-complete problems was also introduced, highligh
0 views • 38 slides
Automatically Generating Algebra Problems: A Computer-Assisted Approach
Computer-assisted refinement in problem generation involves creating algebraic problems similar to a given proof problem by beginning with natural generalizations and user-driven fine-tuning. This process is useful for high school teachers to provide varied practice examples, assignments, and examin
0 views • 16 slides
Fermi Problems and Estimation Techniques in Science
Understand Enrico Fermi's approach to problem-solving through estimation in science as demonstrated by Fermi Problems. These problems involve making educated guesses to reach approximate answers, fostering creativity, critical thinking, and estimation skills. Explore the application of Fermi Problem
0 views • 23 slides
Accelerating Lemma Learning Using Joins in Satisfiability Modulo Theories
Explore the use of joins in accelerating lemma learning within the context of Satisfiability Modulo Theories (SMT). The study covers various SMT applications at Microsoft and delves into the development of the Z3 solver. Key topics include theories, arithmetic operations, array theory, uninterpreted
0 views • 25 slides
Introduction to PDDL Planning Domain Language
PDDL (Planning Domain Description Language) is a language based on STRIPS with various extensions, widely used in the International Planning Competition. It allows for specifying tasks via domain and problem files, representing predicates, operators, objects, initial states, and goal states. Blackbo
0 views • 11 slides
Greedy Algorithms and Optimization Problems Overview
A comprehensive overview of greedy algorithms and optimization problems, covering topics such as the knapsack problem, job scheduling, and Huffman coding. Greedy methods for optimization problems are discussed, along with variations of the knapsack problem and key strategies for solving these proble
0 views • 17 slides
Understanding Signatures, Commitments, and Zero-Knowledge in Lattice Problems
Explore the intricacies of lattice problems such as Learning With Errors (LWE) and Short Integer Solution (SIS), and their relation to the Knapsack Problem. Delve into the hardness of these problems and their applications in building secure cryptographic schemes based on polynomial rings and lattice
0 views • 44 slides
Understanding Decision Problems in Polynomial Time Complexity
Decision problems play a crucial role in computational complexity theory, especially in the context of P and NP classes. These problems involve questions with yes or no answers, where the input describes specific instances. By focusing on polynomial-time algorithms, we explore the distinction betwee
0 views • 32 slides
Bounded Satisfiability Checking for Early Legal Compliance Verification
Early verification of legal compliance is crucial to avoid consequences such as violating regulations like GDPR. Through bounded satisfiability checking using Metric First-order Temporal Logic (MFOTL), this research focuses on system design verification for regulatory compliance. The study addresses
0 views • 29 slides
Understanding SAT Problems and Solution Techniques
Exploring SAT problems and solution techniques such as truth table enumeration, theorem proving, and specialized algorithms for definite clauses. Dive into forward chaining algorithms and their role in solving satisfiability problems efficiently.
0 views • 45 slides
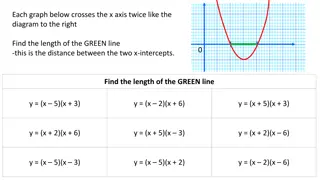
Mathematical Problems Involving Graphs and Equations
The content includes a set of mathematical problems related to graphs, equations, and modeling of paths using given equations. These problems involve finding distances, heights, and intersection points based on the provided graph representations. The scenarios involve water sprinklers watering lawns
0 views • 6 slides
Understanding Constraint Satisfaction Problems and Search
Constraint Satisfaction Problems (CSPs) involve assigning values to variables while adhering to constraints. CSPs are a special case of generic search problems where the state is defined by variables with possible values, and the goal is a consistent assignment. Map coloring is a classic example ill
0 views • 34 slides
Theory of Computation: Decidability and Encoding in CSE 105 Class
Explore the concepts of decidability, encoding, and computational problems in CSE 105 Theory of Computation class. Learn about decision problems, encodings for Turing Machines, framing problems as languages of strings, and examples of computational problems and their encodings. Gain insights into th
0 views • 26 slides
Model-Based Analysis for Identifying Operative Problems at Lelystad Airport
This research study presented at the International Conference on Air Transport 2015 explores the identification of operative problems at Lelystad Airport using a model-based approach. The study aims to develop a model for assessing the future performance of the airport, addressing challenges, and ob
0 views • 27 slides
Surgency as a Person-Level Risk Marker for Externalizing Problems in Children
Surgency is identified as a key interactive risk marker for externalizing problems in children, including Oppositional-Defiant Disorder (ODD) and Attention-Deficit/Hyperactivity Disorder (ADHD). This study explores how high surgency levels, when combined with low effortful control or low A, may incr
0 views • 23 slides
Python_constraint: Solving CSP Problems in Python
Python_constraint is a powerful package for solving Constraint Satisfaction Problems (CSP) in Python. It provides a simple yet effective way to define variables, domains, and constraints for various problems such as magic squares, map coloring, and Sudoku puzzles. This tool offers easy installation
0 views • 21 slides
Insights into NP-Hard Problems in Molecular Biology and Genetics
Understanding the complexity of NP-Hard Problems arising in molecular biology and genetics is crucial. These problems involve genome sequencing, global alignment of multiple genomes, identifying relations through genome comparison, discovering dysregulated pathways in human diseases, and finding spe
0 views • 24 slides
Understanding P, NP, NP-Hard, NP-Complete Problems and Amortized Analysis
This comprehensive study covers P, NP, NP-Hard, NP-Complete Problems, and Amortized Analysis, including examples and concepts like Reduction, Vertex Cover, Max-Clique, 3-SAT, and Hamiltonian Cycle. It delves into Polynomial versus Non-Polynomial problems, outlining the difficulties and unsolvability
0 views • 32 slides
Understanding NP-Hard Problems and NP-Completeness
Delve into the complexities of NP-hard problems, NP-complete problems, and the relationships between NP, NP-hard, and NP-complete classes. Learn about easy-to-verify problems in NP, the concept of NP-completeness, the first NP-complete problem - Gates Circuits, and the NP-complete problem CIRCUIT-SA
0 views • 15 slides
Understanding Z3: An Efficient SMT Solver
Z3 is an efficient Satisfiability Modulo Theories (SMT) solver that integrates various decision procedures for program analysis, verification, and test case generation. It supports linear arithmetic, bit-vectors, uninterpreted functions, quantifiers, and offers an extensive API for different program
0 views • 16 slides
SMT-LIB: The Satisfiability Modulo Theories Library Overview
The Satisfiability Modulo Theories Library (SMT-LIB) is a comprehensive tool for formal reasoning in various supported theories such as arrays, bit vectors, and integer and real arithmetic. It provides a wide range of supported sublogics for precise specifications and verifications. Moonzoo Kim, fro
0 views • 14 slides
Equilibrium and Acid-Base Problems in Chemistry Lecture
In this lecture, topics such as Advanced Equilibrium, Acid/Base Equilibria, Systematic Method for solving chemical problems, Strong Acid/Strong Base scenarios, and General Comments on reactions are discussed. Examples using the systematic method are provided for practical understanding. Key points o
0 views • 13 slides
Evolution of Sociological Perspectives on Social Problems
The study of social problems has evolved dramatically since the 1970s, shifting from an objectivist approach to a more subjective and constructionist perspective. This shift acknowledges that what is considered a social problem is a matter of definition, and focuses on the social processes involved
0 views • 12 slides
Understanding NP-Completeness: Cook-Levin Theorem and Clique Problem
Today's lecture delved into NP-completeness, focusing on the Cook-Levin Theorem and the Clique Problem. NP-completeness is defined as a language that is in NP and all other languages in NP are polynomial-time reducible to it. The Cook-Levin Theorem states that SAT, a Boolean satisfiability problem,
0 views • 10 slides