Portfolio Matrix: Strategic Product Positioning Guide
Learn about the Portfolio Matrix, a strategic tool assessing products based on industry growth and market share. Explore the BCG matrix, its four categories, and how it guides decision-making for products' future success.
1 views • 14 slides
Understanding Composite Materials: Reinforcement and Matrix in Composites
Composite materials consist of reinforcement and matrix components, each serving a specific purpose to enhance the properties of the composite. The reinforcement phase provides strength and stiffness, while the matrix transfers loads and protects the fibers. Different types of reinforcements and mat
8 views • 18 slides
Understanding Extracellular Matrix (ECM) and Its Functions
Extracellular Matrix (ECM) is a complex network of proteins, glycoproteins, and macromolecules that provide structural support, regulate cell activities, and play crucial roles in various tissues. It consists of two main types - interstitial matrix and basement membrane, each serving specific functi
12 views • 25 slides
Understanding the Importance of Completing a Trainer Matrix
Completing a Trainer Matrix is essential for Registered Training Organizations (RTOs) to demonstrate compliance with Standards for RTOs 2015, specifically Clauses 1.13 to 1.16. This matrix outlines requirements for trainers, including holding relevant qualifications, industry skills, and maintaining
2 views • 38 slides
Proposal for Random Access Efficiency Enhancement in IEEE 802.11be Networks
This document presents a proposal for enhancing random access efficiency in IEEE 802.11be networks through a Random-Access NFRP (RA-NFRP) principle. The proposal addresses the challenges of low efficiency in the current UORA procedure and introduces modifications based on the 802.11ax standard to im
5 views • 16 slides
Understanding Bluetooth Low Energy Addresses in IEEE 802.11-21/1535r0
The document explores the features of resolvable addresses in Bluetooth Low Energy (BLE) within the IEEE 802.11-21/1535r0 standard. It discusses the two types of addresses in BLE, Public and Random, and their usage. The emphasis is on Random addresses due to their popularity and privacy features. Th
2 views • 11 slides
Understanding Matrix Organizations and Managing Multiple Principals
Explore the concept of matrix organizations, challenges faced in managing multiple principals, and the importance of accountability, prioritization, and coordination. Learn how matrix structures evolved, their prevalence in modern workforce, and the impact on industries like architecture firms.
1 views • 22 slides
Eisenhower Matrix for Efficient Task Prioritization
Use the Eisenhower Matrix template to effectively prioritize project tasks by distinguishing between urgent and important activities. Delegate, delete, or tackle tasks based on their significance for optimal time management. An example matrix provided showcases various tasks categorized as urgent/im
1 views • 4 slides
Interlock Actions and Matrix for DSS Server in SR1 Environment
Proposal and implementation plan for interlock actions and matrix coordination between DSS server rack and user areas in SR1. Includes agreements, alarms-actions matrix finalization, cable routing, server installation, and commissioning with dummy loads. Discusses CO2 plant signals, temperature moni
4 views • 7 slides
Understanding Matrices in Precalculus: Order, Augmented Matrix, and Row-Echelon Form
Delve into the world of matrices in Precalculus with a focus on identifying matrix orders, creating augmented matrices for systems of equations, transforming matrices into row-echelon form, and solving linear equations using matrices. Explore elementary row operations, row-echelon form, and reduced
1 views • 37 slides
Understanding Random Forests: A Comprehensive Overview
Random Forests, a popular ensemble learning technique, utilize the wisdom of the crowd and diversification to improve prediction accuracy. This method involves building multiple decision trees in randomly selected subspaces of the feature space. By combining the predictions of these trees through a
1 views • 21 slides
Simplifying Random Assignment with The Cambridge Randomizer
The Cambridge Randomizer offers a cost-effective and efficient solution for random assignment in research studies, enabling treatment providers to conduct the process securely. This innovative online portal streamlines the assessment of participant eligibility, provides instant baseline data, and en
0 views • 8 slides
High-Throughput True Random Number Generation Using QUAC-TRNG
DRAM-based QUAC-TRNG provides high-throughput and low-latency true random number generation by utilizing commodity DRAM devices. By employing Quadruple Row Activation (QUAC), this method outperforms existing TRNGs, achieving a 15.08x improvement in throughput and passing all 15 NIST randomness tests
0 views • 10 slides
Understanding Random Variables and Their Applications in Various Fields
Random variables play a crucial role in statistics, engineering, and business applications. They can be discrete or continuous, depending on the nature of the outcomes. Discrete random variables have countable values, while continuous random variables can take on any real number. This article explor
0 views • 6 slides
Understanding Singular Value Decomposition (SVD)
Singular Value Decomposition (SVD) is a powerful method for solving systems of linear equations or matrices that are singular or close to singular. When LU-decomposition or Gaussian elimination fail, SVD provides a stable matrix decomposition helpful in various applications. It is particularly usefu
0 views • 17 slides
Governance Decision Authorities Matrix Overview
A Governance Decision Authorities Matrix is a crucial tool that articulates roles and responsibilities for major decision-making within a system. This template provides a starting point for customizing governance structures, focusing on areas like fiduciary responsibilities, strategic planning, qual
1 views • 9 slides
Understanding the Singular Value Decomposition
The Singular Value Decomposition (SVD) is a powerful factorization method for matrices, extending the concept of eigenvectors and eigenvalues to non-symmetric matrices. This decomposition allows any matrix to be expressed as the product of three matrices: two orthogonal matrices and a diagonal matri
0 views • 35 slides
Understanding Singular Value Decomposition and the Conjugate Gradient Method
Singular Value Decomposition (SVD) is a powerful method that decomposes a matrix into orthogonal matrices and diagonal matrices. It helps in understanding the range, rank, nullity, and goal of matrix transformations. The method involves decomposing a matrix into basis vectors that span its range, id
0 views • 21 slides
Understanding Random Variables and Probability Distributions
Random variables are variables whose values are unknown and can be discrete or continuous. Probability distributions provide the likelihood of outcomes in a random experiment. Learn how random variables are used in quantifying outcomes and differentiating from algebraic variables. Explore types of r
0 views • 13 slides
Understanding Diagonalization in Mathematics
Diagonalization plays a crucial role in converting complex problems into simpler ones by allowing matrices to be represented in a diagonal form. The process involves finding eigenvalues and corresponding eigenvectors, ultimately leading to a diagonal matrix representation. However, careful considera
0 views • 36 slides
Understanding Diagonalization in Linear Algebra
Discover the concept of diagonalization in linear algebra through eigenvectors, eigenvalues, and diagonal matrices. Learn the conditions for a matrix to be diagonalizable, the importance of eigenvectors in forming an invertible matrix, and the step-by-step process to diagonalize a matrix by finding
0 views • 26 slides
Advanced Imputation Methods for Missing Prices in PPI Survey
Explore the innovative techniques for handling missing prices in the Producer Price Index (PPI) survey conducted by the U.S. Bureau of Labor Statistics. The article delves into different imputation methods such as Cell Mean Imputation, Random Forest, Amelia, MICE Predictive Mean Matching, MI Predict
0 views • 22 slides
Understanding Random Class in Java Programming
The Random class in Java is used to generate pseudo-random numbers. By utilizing methods such as nextInt and nextDouble, you can generate random integers and real numbers within specified ranges. This chapter explores common usage scenarios, such as generating random numbers between specific ranges
2 views • 10 slides
Understanding Matrix Factorization for Latent Factor Recovery
Explore the concept of matrix factorization for recovering latent factors in a matrix, specifically focusing on user ratings of movies. This technique involves decomposing a matrix into multiple matrices to extract hidden patterns and relationships. The process is crucial for tasks like image denois
0 views • 50 slides
Understanding Linear Equations and Matrix Operations
Explore the concepts of linear equations, matrix forms, determinants, and finding solutions for variables like x1, x2, x3. Learn about Cramer's Rules, Adjoint Matrix, and calculating the inverse of a matrix through examples and formulas.
0 views • 24 slides
Understanding Random Sampling in Probabilistic System Analysis
In the field of statistical inference, random sampling plays a crucial role in drawing conclusions about populations based on representative samples. This lecture by Dr. Erwin Sitompul at President University delves into the concepts of sampling distributions, unbiased sampling procedures, and impor
0 views • 23 slides
Quantum Key Agreements and Random Oracles
This academic paper explores the impossibility of achieving key agreements using quantum random oracles, discussing the challenges and limitations in quantum communication, cryptographic protocols, quantum computation, and classical communication. The study delves into the implications of quantum ra
0 views • 29 slides
Approximate Inference in Bayes Nets: Random vs. Rejection Sampling
Approximate inference methods in Bayes nets, such as random and rejection sampling, utilize Monte Carlo algorithms for stochastic sampling to estimate complex probabilities. Random sampling involves sampling in topological order, while rejection sampling generates samples from hard-to-sample distrib
0 views • 9 slides
Understanding Random Numbers in Computers
Explore the concept of true random numbers versus pseudorandom numbers in computers. Learn how pseudorandom numbers are generated algorithmically but predictable, while true random numbers are derived from physical phenomena like radioactive decay. Discover the relevance of high-entropy pseudorandom
0 views • 57 slides
IEEE 802.11-21/1585r10: Identifiable Random MAC Address Presentation Summary
This presentation discusses the concept of Identifiable Random MAC (IRM) addresses in the IEEE 802.11-21/1585r10 standard. It covers the purpose of IRM addresses in preventing third-party tracking while allowing trusted parties to identify specific devices. The presentation outlines the use of Ident
0 views • 24 slides
Understanding Laplace Transforms for Continuous Random Variables
The Laplace transform is introduced as a generating function for common continuous random variables, complementing the z-transform for discrete ones. By using the Laplace transform, complex evaluations become simplified, making it easy to analyze different types of transforms. The transform of a con
0 views • 17 slides
Revolutionizing Hotel Communication with Matrix Hospitality Solution
Simplify hotel operations and enhance guest experiences with Matrix Hospitality Solution. From enhancing staff efficiency to boosting revenue generation opportunities, Matrix offers a comprehensive suite of features to meet the diverse needs of hotels. Its modular configuration, scalable platform, a
0 views • 36 slides
Understanding Composite Matrix Materials in Engineering
Composite materials are made of reinforcing fibers and matrix materials, with the matrix serving to protect and enhance the properties of the composite. There are three main types of composite matrix materials: metal matrix composites (MMC), ceramic matrix composites (CMC), and polymer matrix compos
0 views • 22 slides
Understanding Discrete Random Variables and Variance Relationships
Explore the concepts of independence in random variables, shifting variances, and facts about variance in the context of discrete random variables. Learn about key relationships such as Var(X + Y) = Var(X) + Var(Y) and discover common patterns in the Discrete Random Variable Zoo. Embrace the goal of
0 views • 27 slides
Matrix Functions and Taylor Series in Mathematics
A detailed exploration of functions of matrices, including exponential of a matrix, eigenvector sets, eigenvalues, Jordan-Canonical form, and applications of Taylor series to compute matrix functions like cosine. The content provides a deep dive into spectral mapping, eigenvalues, eigenvectors, and
0 views • 53 slides
GUC-Secure Commitments via Random Oracles: New Findings
Exploring the feasibility of GUC-secure commitments using global random oracles, this research delves into the differences between local and global random oracles, outlining motivations and future work. It discusses UC frameworks, zero-knowledge proofs, oblivious transfers, and the GUC framework for
0 views • 18 slides
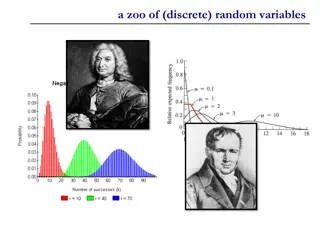
Understanding a Zoo of Discrete Random Variables
Discrete random variables play a crucial role in probability theory and statistics. This content explores three key types: Bernoulli random variable, binomial random variable, and error-correcting codes. From understanding the basics of Bernoulli trials to exploring the application of error correcti
0 views • 27 slides
Parallel Computation for Matrix Multiplication
Matrix multiplication is a fundamental operation with diverse applications across scientific research. Parallel computation for matrix multiplication involves distributing the computational workload over multiple processors, improving efficiency. Different algorithms have been developed for multiply
0 views • 36 slides
Understanding Random Slopes in Data Analysis
Exploring the impact of grand-mean and group-mean centering on intercept interpretation with random slopes, as well as variations in slope/intercept covariance. Differentiating between fixed and random coefficients, and the effects of adding group mean as a Level 2 variable. Delving into within vs.
0 views • 21 slides
Understanding Random Variables and Mean in Statistics
Random variables can be discrete or continuous, with outcomes represented as isolated points or intervals. The Law of Large Numbers shows how the mean of observed values approaches the population mean as the number of trials increases. Calculating the mean of a random variable involves finding the e
0 views • 13 slides