Understanding Principal Components Analysis (PCA) and Autoencoders in Neural Networks
Principal Components Analysis (PCA) is a technique that extracts important features from high-dimensional data by finding orthogonal directions of maximum variance. It aims to represent data in a lower-dimensional subspace while minimizing reconstruction error. Autoencoders, on the other hand, are n
0 views • 35 slides
Understanding the Singular Value Decomposition
The Singular Value Decomposition (SVD) is a powerful factorization method for matrices, extending the concept of eigenvectors and eigenvalues to non-symmetric matrices. This decomposition allows any matrix to be expressed as the product of three matrices: two orthogonal matrices and a diagonal matri
0 views • 35 slides
Understanding Singular Value Decomposition and the Conjugate Gradient Method
Singular Value Decomposition (SVD) is a powerful method that decomposes a matrix into orthogonal matrices and diagonal matrices. It helps in understanding the range, rank, nullity, and goal of matrix transformations. The method involves decomposing a matrix into basis vectors that span its range, id
0 views • 21 slides
Understanding Singular Value Decomposition (SVD) in Linear Algebra
Singular Value Decomposition (SVD) is a powerful technique in linear algebra that breaks down any matrix into orthogonal stretching followed by rotation. It reveals insights into transformations, basis vectors, eigenvalues, and eigenvectors, aiding in understanding linear transformations in a geomet
3 views • 18 slides
Understanding Decomposition of Treatment Sums of Squares
Decomposition of treatment sums of squares involves utilizing prior information about treatment structure to analyze treatment group means through contrasts and hypothesis testing. This process allows for the testing of specific hypotheses and the creation of F-statistics. In an example scenario wit
4 views • 12 slides
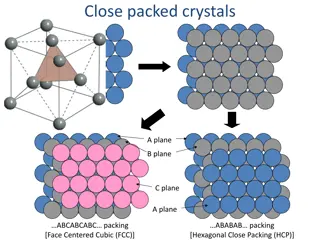
Understanding Crystal Lattice Planes and Indices
Exploring the significance of crystal lattice planes in determining parameters, diffraction methods, and orthogonal systems. Discover how to identify planes and calculate distances in various lattices using Miller indices. Visual aids provide clarity on hexagonal structures and symmetry in crystallo
0 views • 22 slides
An Overview of Evading Anomaly Detection using Variance Injection Attacks on PCA
This presentation discusses evading anomaly detection through variance injection attacks on Principal Component Analysis (PCA) in the context of security. It covers the background of machine learning and PCA, related work, motivation, main ideas, evaluation, conclusion, and future work. The content
1 views • 19 slides
Understanding Eigenvalues in Quantum Information
Explore the eigenvalues of sums of non-commuting random symmetric matrices in the context of quantum information. Delve into the complexities of eigenvalue distributions in various scenarios, including random diagonals, orthogonal matrices, and symmetric matrix sums. Gain insights into classical and
0 views • 24 slides
Understanding Analytic Rotation in Factor Analysis
Factor analysis involves rotation of the factor loading matrix to enhance interpretability. This process was originally done manually but is now performed analytically with computers. Factors can be orthogonal or oblique, impacting the interpretation of factor loadings. Understanding rotation simpli
0 views • 42 slides
Preconditioned Least-Squares Petrov-Galerkin Reduced Order Models Overview
Overview of the approach for model reduction in fluid and solid mechanics problems using Preconditioned Least-Squares Petrov-Galerkin (POD/LSPG). The method involves acquiring, reducing, and solving Ordinary Differential Equations (ODEs) by minimizing the residual through Proper Orthogonal Decomposi
0 views • 30 slides
Applications of Differential Equations in Engineering and Mathematics
Exploring the practical applications of differential equations, specifically focusing on Newton's Law of Cooling and Orthogonal Trajectories. The concept of exact differential equations and their solutions, along with real-life examples demonstrating temperature changes over time, are discussed. Und
0 views • 11 slides
Fundamental Concepts in Vector Spaces and Inner Product Spaces
A vector space over a field F is characterized by operations such as addition and scalar multiplication. Subspaces, direct sums, linear combinations, linear spans, dimensions, and dual spaces are fundamental concepts in vector spaces. Moving into inner product spaces, the concept of inner products,
0 views • 13 slides
Understanding Fractional Factorials in Experimental Designs
Explore the concept of fractional factorials in experimental designs, including the basics, factors, terms estimation, confounding, and practical considerations for running treatment combinations. Learn how to generate incomplete blocks, use orthogonal contrasts, identify confounded terms, and alloc
0 views • 24 slides
Understanding Linear Algebra Concepts: Systems of Equations, Orthogonal Matrix, and Quadratic Forms
Explore the concepts of simultaneous linear equations, homogeneous and non-homogeneous systems, orthogonal matrices, and various types of quadratic forms in linear algebra. Learn about the characteristics of positive definite, semi-positive definite, and negative definite quadratic forms represented
0 views • 7 slides
Understanding the Vector Space Model in Text Mining
Learn how to represent documents computably, infer document relationships, and identify structures using the Vector Space Model. Explore techniques for assigning weights, defining distance metrics, and selecting basic concepts. Discover the importance of orthogonal basic concepts and how they contri
0 views • 43 slides
Understanding Multiple Inheritance in Object-Oriented Programming
Multiple inheritance in object-oriented programming allows a derived class to inherit from more than one base class, creating a unified derived class. This design structure is suitable when the base classes are orthogonal and have no common attributes or behaviors. The derived class logically combin
0 views • 14 slides
Advanced Techniques for Orthogonal Skyline Counting Queries
Advanced techniques for orthogonal skyline counting queries discuss optimal planar solutions, dividing and conquering for topmost point identification, efficient vertical slab counting, succinct data structures for prefix sums and range maxima, upper bounds on degree and multi-slab queries, as well
0 views • 11 slides
IEEE 802.11-17/0044 NDP Short Feedback Design
The document discusses the need for short simultaneous feedback from multiple STAs in IEEE 802.11 systems for improved efficiency. It introduces the NDP feedback mechanism and proposes a signaling technique to efficiently collect feedback from a high number of STAs. The mechanism involves UL MU tran
0 views • 19 slides
Understanding Aerodynamics Fundamentals and Principles
Delve into the world of aerodynamics with an exploration of fundamental principles, equations, flow types, Mach number regimes, and vector relations. Discover the distinctions between inviscid and viscous flows, incompressible and compressible flows, as well as the various Mach number regimes from s
0 views • 17 slides
Evolution of Communication Systems: From Bandwidth Division to Spread Spectrum
Third-generation communication systems utilize Pseudo-Noise (PN) codes to share bandwidth without interference, while first and second-generation systems divide bandwidth into smaller channels. PN codes are vectors with 1s and -1s, orthogonal to each other. Users transmit data using PN coding, combi
0 views • 14 slides
Ensuring Orthogonal Security in Data Encryption Processes
Addressing the challenge of data confidentiality in untrusted server environments through the use of encryption techniques such as deterministic and non-deterministic encryption. The goal is to achieve full functionality independently of data encryption, allowing for secure processing of data querie
0 views • 21 slides
Improved Merlin-Arthur Protocols for Fine-Grained Complexity Problems
The text discusses Merlin-Arthur proof systems and protocols for central problems in fine-grained complexity, particularly focusing on the time complexity, completeness, and soundness of these protocols. It also touches on recent interest in these protocols and presents new results in areas such as
0 views • 16 slides
Classical Algorithms from Quantum and Arthur-Merlin Communication Protocols
Explore the Polynomial Method in classical algorithms, focusing on Orthogonal Vectors, All-Pair-Shortest-Path, and Approximate Closest Pair. Learn how the Polynomial Method works through batch evaluation for multi-variable polynomials and fast matrix multiplication. Discover insights on low-rank dec
0 views • 13 slides