Understanding the Formulation of Hypothesis and Research Problem Definition
Research problems arise from situations requiring solutions, faced by individuals, groups, organizations, or society. Researchers define research problems through questions or issues they aim to answer or solve. Various sources such as intuitions, research studies, brainstorming sessions, and consul
5 views • 25 slides
Understanding The Simplex Method for Linear Programming
The simplex method is an algebraic procedure used to solve linear programming problems by maximizing or minimizing an objective function subject to certain constraints. This method is essential for dealing with real-life problems involving multiple variables and finding optimal solutions. The proces
0 views • 56 slides
Linear Programming Models for Product-Mix Problems and LP Problem Solutions
This unit covers the formulation of linear programming (LP) models for product-mix problems, including graphical and simplex methods for solving LP problems along with the concept of duality. It also delves into transportation problems, offering insights into LP problem resolution techniques.
0 views • 137 slides
Learning Objectives in Mathematics Education
The learning objectives in this mathematics course include identifying key words, translating sentences into mathematical equations, and developing problem-solving strategies. Students will solve word problems involving relationships between numbers, geometric problems with perimeter, percentage and
0 views • 30 slides
Exploring Algorithm Design Approaches with Dr. Jey Veerasamy
Discover a range of algorithm design approaches including quick-sort, merge-sort, divide and conquer characteristics, greedy approach, and solutions to various optimization problems such as petrol cost minimization, number of stops minimization, activity selection, and knapsack problem. Dive into th
0 views • 14 slides
Introduction to Mathematical Programming and Optimization Problems
In optimization problems, one aims to maximize or minimize an objective based on input variables subject to constraints. This involves mathematical programming where functions and relationships define the objective and constraints. Linear, integer, and quadratic programs represent different types of
0 views • 25 slides
Examples of Optimization Problems Solved Using LINGO Software
This content provides examples of optimization problems solved using LINGO software. It includes problems such as job assignments to machines, finding optimal solutions, and solving knapsack problems. Detailed models, constraints, and solutions are illustrated with images. Optimization techniques an
1 views • 41 slides
Formulation of Linear Programming Problems in Decision Making
Linear Programming is a mathematical technique used to optimize resource allocation and achieve specific objectives in decision-making. The nature of Linear Programming problems includes product-mix and blending problems, with components like decision variables and constraints. Various terminologies
1 views • 14 slides
Engaging Mathematics Problems for Critical Thinking and Fun Learning
Explore a collection of engaging mathematics problems and classical brain teasers that challenge students to think critically, problem-solve creatively, and have fun while learning. From dissection tasks to card dealing challenges, these problems encourage students to readjust, reformulate, and exte
0 views • 36 slides
Algorithm Design Techniques: Divide and Conquer
Algorithm design techniques such as divide and conquer, dynamic programming, and greedy algorithms are essential for solving complex problems by breaking them down into smaller sub-problems and combining their solutions. Divide and conquer involves breaking a problem into unrelated sub-problems, sol
1 views • 13 slides
Understanding and Treating Sleep Problems in Children with Autism
Sleep problems in children with autism are viewed as skill deficits that can be addressed through relevant skills teaching. Good sleep is crucial for children's overall well-being, as it affects mood, behavior, learning, and physical health. Lack of good sleep can lead to irritability, fatigue, unin
0 views • 75 slides
Computational Complexity and NP-Complete Problems
In today's discussion, we delved into computational complexity and the challenges faced in finding efficient algorithms for various problems. We explored how some problems defy easy categorization and resist polynomial-time solutions. The concept of NP-complete problems was also introduced, highligh
0 views • 38 slides
Automatically Generating Algebra Problems: A Computer-Assisted Approach
Computer-assisted refinement in problem generation involves creating algebraic problems similar to a given proof problem by beginning with natural generalizations and user-driven fine-tuning. This process is useful for high school teachers to provide varied practice examples, assignments, and examin
0 views • 16 slides
Algorithm Optimization for Knapsack Problem
The homework assignment involves analyzing the performance of two different versions of the Knapsack algorithm by making specific choices regarding item selection. Additionally, a modification to the algorithm is proposed to handle the knapsack problem with unlimited supplies of items, tracking the
0 views • 6 slides
Fermi Problems and Estimation Techniques in Science
Understand Enrico Fermi's approach to problem-solving through estimation in science as demonstrated by Fermi Problems. These problems involve making educated guesses to reach approximate answers, fostering creativity, critical thinking, and estimation skills. Explore the application of Fermi Problem
0 views • 23 slides
Understanding Dynamic Programming for Knapsack Problem and Solutions
Dynamic Programming is a powerful technique used to optimize solutions in the Knapsack Problem by selecting items with maximum value within certain constraints. This approach involves creating a table, making optimal choices, and outputting the best solution. The process is exemplified through a ste
0 views • 11 slides
Understanding the Knapsack Problem and Cryptography
The knapsack problem involves finding a subset of weights that sums up to a given value. It can be applied in cryptographic systems, where superincreasing knapsacks are easier to solve than general knapsacks. The knapsack cryptosystem utilizes superincreasing knapsacks for encryption and conversion
0 views • 14 slides
Understanding the Knapsack Problem in Dynamic Programming
Explore the concept of the Knapsack Problem in dynamic programming, focusing on the 0/1 Knapsack Problem and the greedy approach. Understand the optimal substructure and greedy-choice properties, and learn how to determine the best items to maximize profit within a given weight constraint. Compare t
0 views • 23 slides
Understanding Dynamic Programming in the Context of Knapsack and Edit Distance Problems
This content delves into the Knapsack problem, which involves selecting objects to maximize value while staying within a weight limit, and the Edit Distance problem, which focuses on finding the minimal number of edit operations to convert one string to another. Dynamic programming is used to solve
0 views • 19 slides
Understanding Greedy Algorithms in Algorithmic Design
Greedy algorithms in algorithmic design involve making the best choice at each step to tackle large, complex problems by breaking them into smaller sub-problems. While they provide efficient solutions for some problems, they may not always work, especially in scenarios like navigating one-way street
1 views • 9 slides
Greedy Algorithms for Optimization Problems
The concept of Greedy Algorithms for Optimization Problems is explained, focusing on the Knapsack problem and Job Scheduling. Greedy methods involve making locally optimal choices to achieve the best overall solution. Various scenarios like Huffman coding and graph problems are discussed to illustra
0 views • 28 slides
Overview of Knapsack Cryptosystems and Related Problems
The Merkle-Hellman knapsack cryptosystem is a cryptographic system that was initially proposed by Merkle, and later iterated versions were both broken by Shamir and Brickell in the early 1980s and 1985, respectively. This system is related to the classical knapsack problem, subset-sum problem, and e
0 views • 18 slides
Greedy Algorithms and Optimization Problems Overview
A comprehensive overview of greedy algorithms and optimization problems, covering topics such as the knapsack problem, job scheduling, and Huffman coding. Greedy methods for optimization problems are discussed, along with variations of the knapsack problem and key strategies for solving these proble
0 views • 17 slides
Overview of Public-Key Cryptography and Knapsack Problem in Cryptology
This lecture delves into the realm of public-key cryptography, including the Knapsack one-way function and the Merkle-Hellman Crypto System. It explores historical perspectives, the concepts of OWFs, Elliptic Curve Cryptography, and introduces new algebra using additive groups over Elliptic Curves.
0 views • 16 slides
Dynamic Programming in Discrete Optimization: A Powerful Algorithm Design Technique
Dynamic programming is a powerful algorithm design technique that allows solving complex problems efficiently by breaking them down into overlapping subproblems. This approach, as discussed in the material based on the lectures of Erik Demaine at MIT and Pascal Van Hentenryck at Coursera, involves r
0 views • 69 slides
Approximating Knapsack Problem in Polynomial Time
In the recent discussion, we explored approximating the Knapsack problem in fully polynomial time. By utilizing a polynomial-time approximation scheme (PTAS), we aim to find a set of items within a weight capacity whose value is within a certain range of the optimal value. This approach involves lev
0 views • 22 slides
Optimization Problems and Solutions Using LINGO Programming
Explore optimization problems solved using LINGO programming. Examples include minimizing total job assignment costs, finding optimal solutions, and solving knapsack problems. Follow along with detailed images and instructions for each scenario presented.
0 views • 14 slides
Approximation Algorithms for Stochastic Optimization: An Overview
This piece discusses approximation algorithms for stochastic optimization problems, focusing on modeling uncertainty in inputs, adapting to stochastic predictions, and exploring different optimization themes. It covers topics such as weakening the adversary in online stochastic optimization, two-sta
0 views • 33 slides
0/1 Knapsack Problem by Dynamic Programming: Optimal Solutions for Maximizing Value
Solving the 0/1 Knapsack Problem involves finding the most optimal combination of items to maximize value while staying within a given weight limit. Dynamic Programming (DP) offers a three-step approach to address this optimization challenge efficiently. By calculating the Optimum function and follo
0 views • 5 slides
Understanding Evolutionary Algorithms in Computer Science
Evolutionary algorithms, particularly genetic algorithms, simulate natural evolution to optimize parameters and discover new solutions. By creating genomes representing potential solutions and using genetic operators like mutation and crossover, these algorithms populate a search space, conduct loca
0 views • 33 slides
Understanding Signatures, Commitments, and Zero-Knowledge in Lattice Problems
Explore the intricacies of lattice problems such as Learning With Errors (LWE) and Short Integer Solution (SIS), and their relation to the Knapsack Problem. Delve into the hardness of these problems and their applications in building secure cryptographic schemes based on polynomial rings and lattice
0 views • 44 slides
Understanding Decision Problems in Polynomial Time Complexity
Decision problems play a crucial role in computational complexity theory, especially in the context of P and NP classes. These problems involve questions with yes or no answers, where the input describes specific instances. By focusing on polynomial-time algorithms, we explore the distinction betwee
0 views • 32 slides
Dynamic Programming in Computer Science: Maximizing Smartness on a Plane
Discussing the application of dynamic programming in Computer Science class, specifically solving a problem of maximizing total smartness of students seated in a plane. The discussion covers strategies like memorization, recursion, base cases, and an algorithm to achieve the optimal solution. It als
0 views • 12 slides
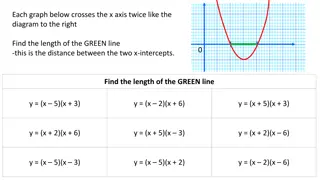
Mathematical Problems Involving Graphs and Equations
The content includes a set of mathematical problems related to graphs, equations, and modeling of paths using given equations. These problems involve finding distances, heights, and intersection points based on the provided graph representations. The scenarios involve water sprinklers watering lawns
0 views • 6 slides
Exploring Dynamic Programming Concepts in Job Scheduling
Delve into the world of dynamic programming by examining the application of segmented least squares, knapsack problems, and job scheduling optimization. Discover the challenges of finding optimal solutions and explore different strategies to address complex scheduling scenarios efficiently.
0 views • 28 slides
Theory of Computation: Decidability and Encoding in CSE 105 Class
Explore the concepts of decidability, encoding, and computational problems in CSE 105 Theory of Computation class. Learn about decision problems, encodings for Turing Machines, framing problems as languages of strings, and examples of computational problems and their encodings. Gain insights into th
0 views • 26 slides
Insights into NP-Hard Problems in Molecular Biology and Genetics
Understanding the complexity of NP-Hard Problems arising in molecular biology and genetics is crucial. These problems involve genome sequencing, global alignment of multiple genomes, identifying relations through genome comparison, discovering dysregulated pathways in human diseases, and finding spe
0 views • 24 slides
Understanding P, NP, NP-Hard, NP-Complete Problems and Amortized Analysis
This comprehensive study covers P, NP, NP-Hard, NP-Complete Problems, and Amortized Analysis, including examples and concepts like Reduction, Vertex Cover, Max-Clique, 3-SAT, and Hamiltonian Cycle. It delves into Polynomial versus Non-Polynomial problems, outlining the difficulties and unsolvability
0 views • 32 slides
Combinatorial Optimization in Integer Programming and Set-Cover Problems
Explore various combinatorial optimization problems such as Integer Programming, TSP, Knapsack, Set-Cover, and more. Understand concepts like 3-Dimensional Matching, SAT, and how Greedy Algorithms play a role. Delve into NP-Hard problems like Set-Cover and analyze the outcomes of Greedy Algorithm se
0 views • 60 slides
Dynamic Programming in Various Algorithms
Jeremy Lin has invented a time machine that predicts $GME stock prices for upcoming days. The challenge is to determine the best trading strategy given the price predictions and constraints on the number of trades allowed. Alongside, there are announcements related to academic activities like homewo
0 views • 36 slides