Exploring FAEST: Post-Quantum Signatures and Zero-Knowledge Proofs
Delve into the world of FAEST, a post-quantum signature scheme, with a focus on publicly verifiable zero-knowledge proofs. The presentation covers VOLE-in-the-Head, families of ZK proofs, and the application of VOLE in creating VOLE-ZK proofs. Learn about the background of VOLE, its use in the desig
1 views • 26 slides
Understanding Inference and Vyapti in Logic
Inference, known as Anumana in Sanskrit, is the process of deriving knowledge based on existing information or observations. It can be used for personal understanding or to demonstrate truths to others. An inference may be SvArtha (for oneself) or ParArtha (for others). Vyapti, the invariable concom
1 views • 14 slides
Understanding Inference in Indian Philosophy
In Indian philosophy, inference is considered one of the six ways to attain true knowledge. It involves three constituents: Hetu (middle term), Sadhya (major term), and Paksha (minor term). The steps of inference include apprehension of the middle term, recollection of the relation between middle an
11 views • 8 slides
Understanding Resolution in Logical Inference
Resolution is a crucial inference procedure in first-order logic, allowing for sound and complete reasoning in handling propositional logic, common normal forms for knowledge bases, resolution in first-order logic, proof trees, and refutation. Key concepts include deriving resolvents, detecting cont
1 views • 12 slides
Understanding the Scope of Inference in Statistical Studies
Statistical studies require careful consideration of the scope of inference to draw valid conclusions. Researchers need to determine if the study design allows generalization to the population or establishes cause and effect relationships. For example, a study on the effects of cartoons on children'
0 views • 15 slides
DNN Inference Optimization Challenge Overview
The DNN Inference Optimization Challenge, organized by Liya Yuan from ZTE, focuses on optimizing deep neural network (DNN) models for efficient inference on-device, at the edge, and in the cloud. The challenge addresses the need for high accuracy while minimizing data center consumption and inferenc
0 views • 13 slides
Mathematical Definitions and Theorems Illustrated
In this collection of images, various mathematical concepts are visually presented, including definitions, theorems, and proofs. The slides cover a range of topics in a structured manner, providing a concise overview of key mathematical principles. From foundational definitions to detailed proofs, t
0 views • 12 slides
Understanding the Difference Between Observation and Inference
Learn to differentiate between observation (direct facts or occurrences) and inference (interpretations based on existing knowledge or experience) through examples such as the Sun producing heat and light (observation) and a dry, itchy skin leading to the inference that it is dry. The distinction be
2 views • 14 slides
Understanding Indirect Proofs: Contradiction and Contraposition Examples
Indirect proofs offer a roundabout approach to proving statements, with argument by contradiction and argument by contraposition being the main techniques. Argument by contradiction involves supposing the statement is false and deriving a contradiction, while argument by contraposition relies on the
1 views • 18 slides
Understanding Algebraic Proofs and Equations
Explore algebraic proofs, equations solving techniques, and properties of equality through examples. Learn about the distributive property, temperature conversion, and problem-solving applications in algebra. Enhance your understanding of logic and algebraic reasoning.
0 views • 30 slides
Navigating Statistical Inference Challenges in Small Samples
In small samples, understanding the sampling distribution of estimators is crucial for valid inference, even when assumptions are violated. This involves careful consideration of normality assumptions, handling non-linear hypotheses, and computing standard errors for various statistics. As demonstra
0 views • 19 slides
Understanding Direct Proofs in Discrete Mathematics
Explore the principles of direct proof in discrete mathematics through a Peer Instruction approach by Dr. Cynthia Bailey Lee and Dr. Shachar Lovett. Learn how to prove theorems of the form "if p, then q" using logical rules, algebra, and math laws. Utilize a clear template for direct proofs, practic
0 views • 17 slides
Guide to Direct Proofs in Discrete Math
Dive into the world of direct proofs in discrete math with this comprehensive guide. Learn how to prove implications, create truth tables, and follow a step-by-step direct proof template. Test your understanding with engaging quizzes and practical examples. Master the art of logical reasoning and fo
0 views • 18 slides
Understanding Rules of Inference in Logic
Dive into the world of logic with this detailed exploration of rules of inference. Learn about different types of arguments, such as Modus Ponens and Modus Tollens, and understand how to determine the validity of an argument. Discover the purpose of rules of inference and unravel the logic behind co
0 views • 17 slides
Evolution of Proofs in Cryptography
Cryptography has evolved from classical proofs to interactive and probabilistically checkable proofs, enabling the development of applications like Non-Malleable and Chosen-Ciphertext Secure Encryption Schemes. Non-Malleability protects against active attacks like malleability and chosen-ciphertext
0 views • 29 slides
Mathematical Proof Techniques and Examples
Explore various proof techniques in mathematics including direct proofs, proofs by cases, proofs by contrapositive, and examples showing how to prove statements using algebra, definitions, and known results. Dive into proofs involving integers, even and odd numbers, and more to enhance your understa
2 views • 13 slides
Algebra and Geometry Reasoning: Concepts and Proofs
Explore key concepts in algebra and geometry reasoning, including properties of equality, distributive property, and proofs using deductive reasoning. Practice solving equations, identifying properties of congruence, and writing two-column proofs to justify mathematical statements.
0 views • 13 slides
Challenges in Constant-Round Public-Coin Zero-Knowledge Proofs
The paper discusses the implausibility of constant-round public-coin zero-knowledge proofs, exploring the limitations and complexities in achieving them. It delves into the fundamental problem of whether such proofs exist, the challenges in soundness error reduction, and the difficulties in parallel
0 views • 20 slides
Understanding Expert Systems and Knowledge Inference
Expert Systems (ES) act as synthetic experts in specialized domains, emulating human expertise for decision-making. They can aid users in safety, training, or decision support roles. Inference rules and knowledge rules play key roles in ES, helping in problem-solving by storing facts and guiding act
0 views • 63 slides
Understanding Knowledge-Based Agents: Inference, Soundness, and Completeness
Inference, soundness, and completeness are crucial concepts in knowledge-based agents. First-order logic allows for expressive statements and has sound and complete inference procedures. Soundness ensures derived sentences are true, while completeness guarantees all entailed sentences are derived. A
0 views • 6 slides
Fast High-Dimensional Filtering and Inference in Fully-Connected CRF
This work discusses fast high-dimensional filtering techniques in Fully-Connected Conditional Random Fields (CRF) through methods like Gaussian filtering, bilateral filtering, and the use of permutohedral lattice. It explores efficient inference in CRFs with Gaussian edge potentials and accelerated
0 views • 25 slides
Probabilistic Graphical Models Part 2: Inference and Learning
This segment delves into various types of inferences in probabilistic graphical models, including marginal inference, posterior inference, and maximum a posteriori inference. It also covers methods like variable elimination, belief propagation, and junction tree for exact inference, along with appro
0 views • 33 slides
Advancements in Interactive Proofs for Efficient Computation
Recent developments in interactive proofs focus on enhancing the efficiency of computations outsourced to untrusted servers, addressing concerns related to correctness and privacy. Solutions like doubly efficient interactive proofs offer a secure way to delegate computations while minimizing relianc
0 views • 25 slides
Optimizing Inference Time by Utilizing External Memory on STM32Cube for AI Applications
The user is exploring ways to reduce inference time by storing initial weight and bias tables in external Q-SPI flash memory and transferring them to SDRAM for AI applications on STM32Cube. They have questions regarding the performance differences between internal flash memory and external memory, r
0 views • 4 slides
Understanding Exhaustive Proofs and Proof by Cases in Discrete Math
Exhaustive proofs and proofs by cases are essential methods in discrete mathematics for proving theorems. Exhaustive proofs involve checking all possibilities, while proof by cases focuses on considering different scenarios separately. The methods are illustrated through examples like proving (n+1)^
0 views • 8 slides
Evolution of Proofs in Computer Science
Explore the development of proofs in computer science, from classical mathematical proofs to interactive and zero-knowledge proofs pioneered by researchers like Goldwasser, Micali, Rackoff, and others. Discover how proof theory has evolved over time, making computation verification more efficient an
0 views • 28 slides
Constant Round Interactive Proofs for Delegating Computations
The research explores techniques for securely delegating computations to the cloud, addressing concerns of correctness and privacy through interactive proofs and efficient verification methods. It compares classical and doubly efficient interactive proofs, emphasizing the importance of computational
0 views • 43 slides
Typed Assembly Language and Type Inference in Program Compilation
The provided content discusses the significance of typed assembly languages, certifying compilers, and the role of type inference in program compilation. It emphasizes the importance of preserving type information for memory safety and vulnerability prevention. The effectiveness of type inference me
0 views • 17 slides
Evolution of Proofs in Computer Science: Zero-Knowledge Proofs Overview
Explore the evolution of proofs in computer science focusing on succinct zero-knowledge proofs, their significance, and impact on Bitcoin protocol and public ledgers. Learn about classical proofs, zero-knowledge proofs by Goldwasser-Micali-Rackoff, and interactive proofs in the realm of computer sci
0 views • 40 slides
Rules of Inference Exercise Solutions in Discrete Math
This content provides solutions to exercises involving rules of inference in discrete mathematics. The solutions explain how conclusions are drawn from given premises using specific inference rules. Examples include identifying whether someone is clever or lucky based on given statements and determi
0 views • 4 slides
Modern Likelihood-Frequentist Inference: A Brief Overview
The presentation by Donald A. Pierce and Ruggero Bellio delves into Modern Likelihood-Frequentist Inference, discussing its significance as an advancement in statistical theory and methods. They highlight the shift towards likelihood and sufficiency, complementing Neyman-Pearson theory. The talk cov
0 views • 22 slides
Understanding Predicate Logic and Quantifiers for Symbolic Proofs
Dive into the realm of predicate logic and quantifiers, exploring the nuances of symbolic proofs and evaluating logical statements. Learn about bound variables, domain considerations, and strategies for constructing iron-clad proofs using quantifiers.
0 views • 36 slides
Quantum NIZK Proofs Explained with Dominique Unruh
Explore the concept of non-interactive quantum zero-knowledge proofs with Dominique Unruh at the University of Tartu. Discover how these proofs ensure verifier acceptance of true statements while learning nothing, and delve into the various implementations and implications of Quantum NIZK proofs wit
0 views • 19 slides
Zero-Knowledge Proofs in Cryptography
Exploring zero-knowledge proofs in cryptography, this content delves into interactive protocols, perfect zero-knowledge definitions, and the QR protocol's honest verifier and malicious verifier zero-knowledge theorems. It discusses how simulators work to maintain zero-knowledge properties and the si
0 views • 37 slides
Sequential Approximate Inference with Limited Resolution Measurements
Delve into the world of sequential approximate inference through sequential measurements of likelihoods, accounting for Hick's Law. Explore optimal inference strategies implemented by Bayes rule and tackle the challenges of limited resolution measurements. Discover the central question of refining a
0 views • 29 slides
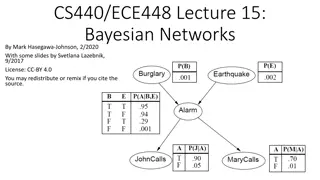
Understanding Bayesian Networks for Efficient Probabilistic Inference
Bayesian networks, also known as graphical models, provide a compact and efficient way to represent complex joint probability distributions involving hidden variables. By depicting conditional independence relationships between random variables in a graph, Bayesian networks facilitate Bayesian infer
0 views • 33 slides
Interactive Proofs in Complexity Theory
Delve into the realm of interactive proofs in complexity theory, exploring concepts such as completeness, soundness, and efficiency. Discover how interactive proof systems can be utilized in scenarios like graph isomorphism and their implications on the complexity classes NP and coNP. Uncover the in
0 views • 40 slides
Predicate Logic and Proofs in CSE 311
Explore the translation of statements into predicate logic, learn about inference proofs and nested quantifiers, and delve into the application of logical thinking in real-world scenarios. Discover a new way of constructing proofs and understand notation laws of inference. Engage in interactive proo
0 views • 37 slides
Dynamic Crowd Simulation Using Deep Reinforcement Learning and Bayesian Inference
This paper introduces a novel method for simulating crowd movements by combining deep reinforcement learning (DRL) with Bayesian inference. By leveraging neural networks to capture complex crowd behaviors, the proposed approach incorporates rewards for natural movements and a position-based dynamics
0 views • 15 slides
Understanding Mathematical Proofs and Concepts
Explore the world of mathematical proofs through chapters 4, 5, and 6. Delve into terminology, theorems, definitions, divisors, and accepted axioms used in mathematical reasoning. Discover the logic behind proofs and various methods employed in establishing the truth of mathematical statements.
1 views • 101 slides