Euclidean - PowerPoint PPT Presentation

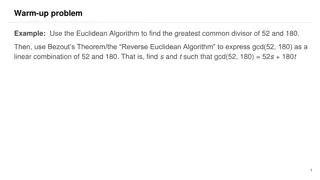
Exploring concepts of linear congruences using examples like finding times congruent to 2 o'clock and applying the Euclidean Algorithm to determine the greatest common divisor of 52 and 180. Learn about Bezout's Theorem for expressing GCD as a linear combination of the given numbers.

0 views • 26 slides

Multidimensional scaling (MDS) aims to represent similarity or dissimilarity measurements between objects as distances in a lower-dimensional space. Principal Coordinates Analysis (PCoA) and other unsupervised learning methods like PCA are used to preserve distances between observations in multivari

4 views • 21 slides

This project focuses on multi-person 3D human pose estimation from monocular images using advanced techniques like HG-RCNN for 2D heatmaps estimation and a shallow 3D pose module for lifting keypoints to 3D space. The approach leverages weak-perspective projection assumptions for global pose approxi

0 views • 8 slides

Dive into the fascinating world of hyperbolic geometry, where angles in a triangle are less than 180 degrees and tilings exhibit negative curvature. Discover the beauty of the Hyperbolic Plane and learn about regular hyperbolic tilings characterized by Schlafli Symbols. Explore different models like

0 views • 46 slides

This study explores the use of complex time methods and chameleon scalar fields in understanding and modeling spatial extremes in hydrological and atmospheric systems. By transforming Lagrangian processes and introducing chameleon scalar fields, the research unveils new insights into the mechanism g

0 views • 9 slides

Learn about the concept of greatest common divisors (GCD), how to compute them efficiently using the Euclidean Algorithm, the Quotient-Remainder Theorem, and the properties of common divisors. Explore examples and applications of GCD, extending to linear combinations, prime factorization, and other

0 views • 45 slides

This text delves into the fundamental concepts of number theory, divisibility, and finite fields essential for understanding cryptography. It covers topics such as divisibility, properties of divisibility, the division algorithm, the Euclidean algorithm for determining the greatest common divisor, a

0 views • 35 slides

Background on the use of number theory in constructing key exchange protocols, digital signatures, and public-key encryption. Covers notation, modular arithmetic, greatest common divisor, modular inversion, invertible elements, and solving modular linear equations efficiently using the extended Eucl

0 views • 45 slides

Explore the concept of clustering data points in high-dimensional spaces with distance measures like Euclidean, Cosine, Jaccard, and edit distance. Discover the challenges of clustering in dimensions beyond 2 and the importance of similarity in grouping objects. Dive into applications such as catalo

0 views • 55 slides

Explore the world of math through workshops, activities, and project presentations at PMEG 2023. Dive into Euclidean Geometry, straight lines, Monopoly, Fibonacci, Cartesian Planes, linear equations, and binary code with our dynamic teams. Unveil the possibilities of mathematical exploration!

0 views • 5 slides

Delve into the fascinating world of General Relativity as we discuss the equivalence principle, gravitational waves, properties of spacetime, and the effects of curvature in the presence of gravity. Discover how Einstein's revolutionary theories have reshaped our understanding of the universe, leadi

0 views • 15 slides

Explore the realms of Euclidean, Hyperbolic, and Elliptic geometries along with their unique characteristics, axioms, and the implications of the parallel postulates. Delve into the distinctions between these geometries and the intriguing concept of mixing Euclidean and Hyperbolic geometries within

1 views • 6 slides

Explore the foundations of Euclidean Geometry, delve into the Pythagorean Theorem, discover the postulates of Euclid, and learn about distance functions, Euclidean distance, taxi-cab metric, circles, and isometries and congruence. Unravel the rich history, key principles, and practical applications

1 views • 37 slides

Cluster analysis is a vital method in statistical data analysis that aims to identify subgroups within a population based on similarities between observations. It involves techniques like building regression models for supervised learning and utilizing distance measures for assessing dissimilarity.

0 views • 25 slides

Explore the fundamentals of vectors, matrices, rotations, and coordinate transformations in Euclidean space. Learn about points, tensors, and the significance of vectors in representing physical quantities. Discover the Parallelogram Law and Coordinate Frames for effective visualization and computat

0 views • 46 slides

The discussion explores Weyl quantum mechanics, Bohm's interpretation of quantum potential, and geometric formulations in Euclidean-Weyl space. It delves into the implications of nonlocal quantum potentials and the nature of metric spaces in shaping quantum phenomena. Concluding with alternative vie

0 views • 30 slides

This chapter delves into using Python lists for data storage, implementing data mining applications, and exploring cluster analysis. Learn about clusters, centroids, Euclidean distance, visualization, and how to write functions for data analysis. The concepts of indefinite iteration and loop control

2 views • 27 slides

A matched control group consists of customers similar to those in a treatment group but not subjected to the treatment. This methodology is useful when an experimentally designed control group is unavailable, there is a large pool of eligible control customers, or the treatment is not event-based. T

1 views • 12 slides

This study explores a method to defend against adversarial images by approximating their projection onto the image manifold through nearest-neighbor search. The approach involves finding the nearest neighbors in a web-scale image database to classify and mitigate the impact of adversarial perturbati

0 views • 15 slides

Euclidean Path Integral & Statistical Ensembles cover topics such as phase transitions, regularity conditions, and gauge potential regularity. In Quantum Field Theory, the path integral is defined and governed by saddle point approximation, leading to thermodynamic quantities like internal energy an

0 views • 57 slides

Unlock the complexities of Euclidean Path Integral in Dyonic Taub-NUT-AdS Phases and delve into thermal field theory, gauge potential regularity, statistical ensembles, and phase transitions. Explore the nuances of quantum field theory and the fascinating world of gravitational metrics. Discover the

0 views • 22 slides

Delve into the fascinating principles of general relativity, including the equivalence of gravitational and inertial mass, the apparent curvature of light, gravitational lensing, and the mysterious nature of black holes. Explore how mass distorts space and the non-Euclidean geometry underlying our u

0 views • 29 slides

This paper delves into the fascinating realm of operator scaling discussed by Yuanzhi Li from Princeton University in collaboration with other researchers. The focus is on group actions and problems related to orbit intersection, offering insight into graph isomorphism, complexity levels, and an eff

0 views • 60 slides

This content delves into the exploration of treating points as vectors in a homogeneous viewpoint, emphasizing the significance of preserving geometric meaning despite scaling. It discusses the direct interpretation of the inner product of vectors as the distance between points, aiming to meet vario

0 views • 24 slides

This content delves into memory-based learning with a focus on nearest neighbor algorithms. It covers topics like distance metrics, number of neighbors, weighting functions, and local point fitting. Visual representations and examples enhance the discussion, offering insights into regression and mul

0 views • 24 slides

Dive into the intricate world of Uniform Semimodular Lattices and Valuated Matroids as discussed in the research by Hiroshi Hirai at the University of Tokyo. Explore the connections to Euclidean building and combinatorial geometries, offering a fresh perspective on geometric structures and matroid t

0 views • 25 slides

Learn about representing images as vectors, calculating distances using Euclidean and Manhattan methods, and classifying images with the nearest neighbor algorithm. Understand the vector representation of images and the concepts of Euclidean and Manhattan distances. Explore the nearest neighbor clas

0 views • 35 slides

This course covers advanced algorithms for handling big data, focusing on topics such as Euclidean space, CountSketch, ?2 estimation, moment estimation, Johnson-Lindenstrauss lemma, and algorithm implementation. Dive into the intricacies of Euclidean space, distance functions, heavy-hitters problems

0 views • 35 slides

This paper delves into the geometric complexities of constructing the orbit of Mercury, exploring Galilean energy curves to rectify perceived irregularities in square space ellipses. Through Euclidean and analytic geometry, alongside elementary calculus, a curved space perception is introduced to ap

0 views • 13 slides

Geostatistics, a branch of statistics focusing on spatial datasets, plays a crucial role in various disciplines like geology, hydrology, and agriculture. Tobler's First Law of Geography forms the foundation of spatial analysis, emphasizing the relationship between proximity and interaction in spatia

0 views • 6 slides

This research presented at SODA 2021 introduces a solution for finding the shortest Euclidean path between two points in a free space containing polygonal obstacles. By dividing the algorithm into phases and using persistent binary trees, the space complexity is reduced to O(n log n), significantly

0 views • 15 slides

Learn about norms and metrics in vector spaces through topics such as similarity of vectors, Minkowski norm, cosine similarity, Euclidean distance, and Minkowski distance. Discover the fundamental properties of norms, distance calculations between vectors, and applications in metric learning.

1 views • 26 slides

Explore the concepts of pixels relationships, different distance measures, and the application of these measures in digital image analysis. Learn about foreground and background regions, distance functions, and distance formulas such as Euclidean Distance and City-Block Distance.

0 views • 29 slides

Delve into the concept of black hole information emissions through quantum extremal surfaces, the subtleties of interpreting path-integrals, and embedding images into orthodox path integral formulations. Follow the Euclidean path-integral approach, analyze steepest-descent approximations, and explor

0 views • 45 slides

Explore the k-means clustering algorithm and other prominent techniques in machine learning. Dive into the similarities, differences, advantages, and disadvantages of algorithms like k-means++, canopy clustering, and farthest-first clustering. Learn about essential distance metrics such as Euclidean

0 views • 8 slides

Explore the concept of clustering in big data processing, covering topics such as distance measures, algorithmic approaches, and the challenges of high-dimensional data. Learn about hierarchical clustering, point assignment algorithms, and different distance measures like Euclidean, Jaccard, and Cos

0 views • 50 slides

Explore the concepts of classification using K-Nearest Neighbor, distance measures, and properties of distance in supervised and unsupervised learning. Learn about different distance metrics such as Euclidean, Manhattan, Hamming, and Mahalanobis distances, and their applications in measuring similar

0 views • 28 slides

Delve into the recent progress on black hole information, exploring the concept of quantum extremal surfaces in an evaporating black hole spacetime, and the implications for unitarity and Hawking radiation. Discover the role of Euclidean wormholes and the gravitational path integral in shedding ligh

0 views • 16 slides

Explore the paper on privately comparing regions in Euclidean space for validating sensor outputs, with applications in collaborative obstacle detection for connected autonomous vehicles. The research addresses the challenge of maintaining trust and privacy among different manufacturers while ensuri

0 views • 17 slides

Explore various concepts in Euclidean space such as distances, vectors, dot products, and collinearity, illustrated with examples and visuals.

0 views • 21 slides