Bivariate Normal Data Analysis: LPGA 2008 Season Overview
Explore the analysis of bivariate normal data focusing on LPGA driving distance and fairway percent from the 2008 season. Learn how to compute confidence ellipses, estimated means, variance-covariance matrix, eigenvalues, eigenvectors, and plot insightful visualizations. Understand the method, set u
1 views • 8 slides
Singular Value Decomposition
The Singular Value Decomposition (SVD) is a powerful factorization method for matrices, extending the concept of eigenvectors and eigenvalues to non-symmetric matrices. This decomposition allows any matrix to be expressed as the product of three matrices: two orthogonal matrices and a diagonal matri
0 views • 35 slides
Singular Value Decomposition (SVD) in Linear Algebra
Singular Value Decomposition (SVD) is a powerful technique in linear algebra that breaks down any matrix into orthogonal stretching followed by rotation. It reveals insights into transformations, basis vectors, eigenvalues, and eigenvectors, aiding in understanding linear transformations in a geomet
3 views • 18 slides
Eigenvalues and Characteristic Polynomials
Unravel the mystery of eigenvalues and characteristic polynomials through detailed lectures and examples by Hung-yi Lee. Learn how to find eigenvalues, eigenvectors, and eigenspaces, and explore the roots of characteristic polynomials to solve characteristic equations. Dive into examples to discover
2 views • 19 slides
Diagonalization in Mathematics
Diagonalization plays a crucial role in converting complex problems into simpler ones by allowing matrices to be represented in a diagonal form. The process involves finding eigenvalues and corresponding eigenvectors, ultimately leading to a diagonal matrix representation. However, careful considera
0 views • 36 slides
Eigenvalues and Eigenvectors in Linear Algebra
Explore the concepts of eigenvectors and eigenvalues in linear algebra, from defining orthonormal bases and the Gram-Schmidt process to finding eigenvalues of upper triangular matrices. Learn the theorems and examples that showcase the importance of these concepts in matrix operations and transforma
0 views • 24 slides
Diagonalization in Linear Algebra
Discover the concept of diagonalization in linear algebra through eigenvectors, eigenvalues, and diagonal matrices. Learn the conditions for a matrix to be diagonalizable, the importance of eigenvectors in forming an invertible matrix, and the step-by-step process to diagonalize a matrix by finding
1 views • 26 slides
Low Threshold Rank Graphs and Their Structural Properties
Explore the intriguing world of low threshold rank graphs and their structural properties, including spectral graph theory, Cheeger's inequality, and generalizations to higher eigenvalues. Learn about the concept of threshold rank, partitioning of graphs, diameter limits, and eigenvectors approximat
0 views • 22 slides
Principal Component Analysis (PCA) in Data Analysis
Introduction to Principal Component Analysis (PCA) by J.-S. Roger Jang from MIR Lab, CSIE Dept., National Taiwan University. PCA is a method for reducing dataset dimensionality while preserving spatial characteristics. It has applications in line/plane fitting, face recognition, and machine learning
0 views • 23 slides
Eigenvectors in Linear Algebra
Explore the concept of eigenvectors in linear algebra, covering topics such as linear transforms, eigenvalues, symmetric matrices, and their practical applications. Learn how eigenvectors represent directions in which a transformation only stretches or compresses without changing direction, and unde
1 views • 25 slides
Matrix Functions and Taylor Series in Mathematics
A detailed exploration of functions of matrices, including exponential of a matrix, eigenvector sets, eigenvalues, Jordan-Canonical form, and applications of Taylor series to compute matrix functions like cosine. The content provides a deep dive into spectral mapping, eigenvalues, eigenvectors, and
0 views • 53 slides
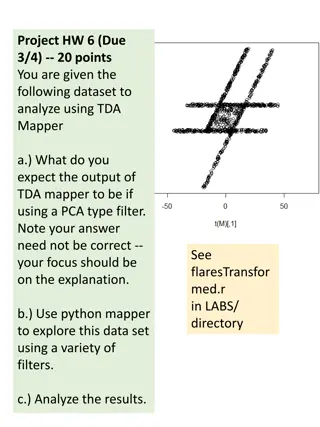
Data Analysis Using TDA Mapper - Exploring Filters and Results
Use of TDA Mapper to analyze datasets, focusing on different filters like PCA, distance matrix eigenvectors, and kNN. Understand how varying intervals affect cluster detection and learn from the analysis of clustering results.
0 views • 6 slides
Multiplication-Avoiding Variant of Power Iteration with Applications
This study introduces a novel approach called Multiplication-Avoiding Variant of Power Iteration (MAPI) and its applications in the context of Reproducing Kernel Hilbert Space. The method is designed to efficiently compute dominant eigenvectors without conventional matrix multiplications, utilizing
0 views • 13 slides
Principal Components Analysis for Detecting Major Data Variations
Principal Components Analysis (PCA) is a powerful method for identifying significant directions of variation in data sets. It is particularly adept at revealing hidden structures like population subgroups with diverse allele frequencies and uncovering unexpected relationships or errors. By performin
0 views • 20 slides
Eigenvalues and Eigenvectors in Linear Algebra
Eigenvalues and eigenvectors are fundamental concepts in linear algebra, essential for solving problems related to matrices and transformations. This content delves into the geometric interpretation, verification of eigenvalues, eigenvectors, eigenspaces, and examples of eigenspaces on the xy-plane.
0 views • 73 slides
Matrix Models of Base Substitutions II: Eigenvalues and Eigenvectors
Exploring matrix models in mathematical modeling, focusing on base substitutions. Reviewing Markov models, understanding characteristic polynomials, eigenvectors, and eigenvalues. Discussing geometric meanings, Lemmas, and base distribution vectors estimation using transition matrices. Assumptions i
0 views • 45 slides
Matrix Models of Base Substitutions II
Review of Markov models, eigenvalues, and eigenvectors in the context of base substitutions. Explore the geometric meaning of eigenvalues and eigenvectors, along with the application of transition matrices in estimating base distribution vectors. Dive into the fundamental assumptions of Markov model
1 views • 15 slides
Understanding Stability of Fixed Points in Classical Mechanics and Electromagnetism
Explore the concept of fixed points in phase-space, their stability, and linearization for stability analysis in classical mechanics and electromagnetism. Learn how to identify stable and unstable fixed points using vector diagrams and eigenvalues. Gain insights into the motion near fixed points and
0 views • 14 slides
Explore Linear Algebra Course Details and Benefits
Delve into the intriguing world of Linear Algebra with this comprehensive course covering key topics such as matrices, vectors, systems of equations, determinants, eigenvalues, eigenvectors, and more. Understand the advantages and disadvantages of linear concepts, and discover how algebra plays a cr
0 views • 26 slides
ECE 417 Lecture 9: Exam 1 Review Highlights
Dive into the review highlights for Exam 1 in ECE 417 with topics including distance metrics, Minkowski norms, Mahalanobis distance, Gaussian distributions, eigenvectors, classifiers, and more. Get ready for the upcoming exam by exploring key concepts covered in the course material.
0 views • 30 slides
Understanding Eigenvalues and Eigenvectors in Linear Algebra
Explore the concepts of eigenvalues and eigenvectors in linear algebra through discussions on eigenvalue problems, geometric interpretation, eigenspaces, and applications. Delve into diagonalization, symmetric matrices, and principal component analysis for a comprehensive understanding.
0 views • 79 slides
Understanding Eigenvalues and Eigenvectors in Linear Algebra
Explore the concept of eigenvalues and eigenvectors in linear algebra with examples and theorems. Understand how eigenvalues relate to matrix transformations and eigenvectors form subspaces in Rn, illustrated through geometric interpretations.
0 views • 73 slides
Understanding Diagonal Matrices and Diagonalization in Linear Algebra
Dive into the world of diagonal matrices - learn what they are, how they affect vectors, and explore diagonalization using eigenvalues and eigenvectors. Discover the significance of diagonalizable matrices and their properties.
0 views • 57 slides