Famous Sexologist in Patna and Lakhisarai over phone | Dr. Sunil Dubey
Do you live in Lakhisarai city which is the administrative headquarters of Lakhisarai district in Bihar, India? Actually, this city is famous for its Ashok Dham temple in India. Right now you are sad because of your sexual problem. This sexual problem not only troubles you but is also spoiling your
17 views • 6 slides
Solving the Missionaries and Cannibals River Crossing Problem
Consider the classic problem of three missionaries and three cannibals needing to cross a river using a canoe that can hold up to two people. The challenge is to transport everyone safely without leaving more cannibals than missionaries on either side of the river. Learn about search problem formula
0 views • 124 slides
Understanding the LIBRE Model Stick Figure Tool for Scoring and Engagement Style Analysis
The LIBRE Model Stick Figure Tool is designed for problem-solving exchanges between a problem-solver and a facilitator. It involves five prompts - Listen, Identify, Brainstorm, Reality-test, and Encourage - aimed at self-reflection and behavior modification. The model emphasizes self-regulated atten
0 views • 34 slides
Comprehensive Overview of Problem-Oriented Medical System in Physiotherapy Assessment
In the realm of physiotherapy assessment, the Problem-Oriented Medical System (POMS) plays a vital role in accurately defining patient problems, creating treatment plans, and monitoring progress. This system, pioneered by Weed in 1968, consists of Problem-Oriented Medical Records (POMR), auditing, a
2 views • 34 slides
Engaging Paper-Based Problem Solving for Computational Thinking Skills
Implementing paper-based problem-solving activities using puzzles, riddles, and pattern recognition can effectively introduce computational thinking without the need for complex technology or terminology. Through real-life scenarios like transporting a fox, chicken, and corn across a river or encodi
0 views • 23 slides
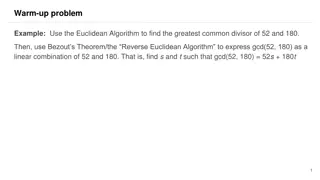
Understanding Linear Congruences and the Euclidean Algorithm in Number Theory
Exploring concepts of linear congruences using examples like finding times congruent to 2 o'clock and applying the Euclidean Algorithm to determine the greatest common divisor of 52 and 180. Learn about Bezout's Theorem for expressing GCD as a linear combination of the given numbers.
0 views • 26 slides
Mastering Fraction Division with Dr. Emerlina C. Binuya
Explore the step-by-step process of dividing fractions and whole numbers with expert guidance from Dr. Emerlina C. Binuya. Learn how to invert the divisor, convert the division sign to multiplication, cross-cancel, multiply numerators and denominators, and convert improper fractions to mixed numbers
0 views • 6 slides
Understanding Complex Computing Problem (CCP) and Complex Computing Activity (CCA)
Dr. Saman Hina, along with Dr. Farrukh Arif and Dr. Maria Waqas, presents information on Complex Computing Problem (CCP) - a problem involving technical, computing, and other issues with no obvious solution, requiring deep knowledge and analytical thinking. CCP is evaluated through predefined rubric
4 views • 19 slides
Overview of Research Problem Identification and Formulation
Understanding the importance of defining a research problem, this content delves into the selection and formulation of research problems, the definition of a research problem, reasons for defining it, methods for identifying research problems, sources of research problems, and considerations in sele
1 views • 11 slides
Understanding the MECE Framework for Efficient Problem-Solving
The MECE (Mutually Exclusive, Collectively Exhaustive) framework is a powerful tool used by business leaders and consultants like McKinsey to structure information, reduce complexity, and gather comprehensive data without overlaps. It involves creating issue trees that subdivide problem elements int
1 views • 4 slides
Uninformed Search Chapter 3 - Goal-based Agents and Problem Solving
Discussing goal-based agents and problem solving in artificial intelligence, the chapter covers topics such as representing states and actions, various search algorithms like breadth-first and depth-first search, as well as the problem space principle developed by Allen Newell and Herb Simon. Exampl
2 views • 52 slides
Solving the Professors to Coffee Lounge Problem: A Graph Theory Approach
An intriguing mathematical problem is presented where new faculty members at TIMS must be assigned to coffee lounge alcoves in a way that ensures no two new members meet after the first day. By constructing a graph based on meet-up timings, analyzing clashes, and determining intervals, this scenario
1 views • 19 slides
Divide and Conquer: A Strategy for Problem Solving
Divide-and-conquer is a powerful problem-solving technique in Computer Science where a large problem is divided into smaller sub-problems, conquered individually, and then combined to solve the original problem. Through three steps - Divide, Conquer, and Combine - complex problems can be efficiently
3 views • 18 slides
Understanding Arithmetic Statistics in Function Fields
Delve into the world of arithmetic statistics in function fields, exploring concepts like the Divisor function, Dirichlet divisor problem, counting methods, Euler summation formula, and more. Discover the beauty of number theory through the lens of these mathematical functions and distributions.
0 views • 22 slides
Understanding Linear Combinations and Common Divisors Theorem
Exploring the relationship between linear combinations and common divisors through the theorem connecting the greatest common divisor (GCD) and the smallest positive integer linear combination (SPC) of two integers a and b. The theorem states that the GCD is less than or equal to the SPC, with proof
0 views • 45 slides
Understanding Greatest Common Divisor and Euclidean Algorithm
Learn about the concept of greatest common divisors (GCD), how to compute them efficiently using the Euclidean Algorithm, the Quotient-Remainder Theorem, and the properties of common divisors. Explore examples and applications of GCD, extending to linear combinations, prime factorization, and other
0 views • 45 slides
Understanding Properties of Integers in Number Theory
Exploring fundamental concepts in number theory such as divisors, the divisor theorem, prime numbers, and the fundamental theorem of arithmetic. Discover the significance of integer properties in encryption algorithms and their practical applications in modern times.
0 views • 42 slides
Basics of Division in Number Theory and Encryption
Understanding arithmetic operations for discrete numbers is crucial in the world of Number Theory and Encryption. This session covers the fundamentals of addition, subtraction, multiplication, and division, emphasizing key terms like dividend, numerator, divisor, quotient, remainder, and fraction. T
0 views • 7 slides
Understanding Cryptography: Basic Concepts in Number Theory and Divisibility
This text delves into the fundamental concepts of number theory, divisibility, and finite fields essential for understanding cryptography. It covers topics such as divisibility, properties of divisibility, the division algorithm, the Euclidean algorithm for determining the greatest common divisor, a
0 views • 35 slides
Understanding Euclid's Algorithm: An Ancient Approach to Finding Greatest Common Divisors
Euclid's Algorithm, dating back 2500 years, offers a simpler method to find the greatest common divisor (gcd) of two non-negative integers compared to traditional factorization. By iteratively applying a rule based on the gcd of remainders, it efficiently computes gcd values. The basis of the algori
0 views • 15 slides
Polynomial Division Methods and Examples
Dividing polynomials involves using methods like long division or equating coefficients. By applying these techniques, you can determine whether a polynomial divides exactly or leaves a remainder. The process is similar to long division of numbers, where the dividend is divided by the divisor to obt
0 views • 10 slides
Cryptography and Number Theory Crash Course
Background on the use of number theory in constructing key exchange protocols, digital signatures, and public-key encryption. Covers notation, modular arithmetic, greatest common divisor, modular inversion, invertible elements, and solving modular linear equations efficiently using the extended Eucl
0 views • 45 slides
Basic Concepts in Number Theory and Finite Fields for Cryptography
In this presentation, the basic concepts of number theory, including divisors, properties of divisibility, the division algorithm, and the greatest common divisor (GCD), are explored in the context of cryptography and network security. The importance of finite fields in cryptographic operations such
0 views • 38 slides
Comprehensive Guide to Problem Oriented Medical Record (POMR) and Master Problem Lists
Delve into the world of Problem Oriented Medical Records (POMR) and Master Problem Lists (MPL) through the insightful teachings of Dr. Lawrence Weed. Learn the systematic approach, SOAP writing, and the significance of maintaining a patient-focused perspective. Understand the challenges in diagnosis
0 views • 35 slides
Mastering Partial Quotients Method for Easy Multiplication Practice
Enhance your students' math skills with the Partial Quotients method, focusing on multiples of ten and finding simple multiples of the divisor. This visual guide showcases step-by-step examples to help students build proficiency in division using easy-to-understand illustrations.
0 views • 31 slides
Understanding the Knapsack Problem in Dynamic Programming
Explore the concept of the Knapsack Problem in dynamic programming, focusing on the 0/1 Knapsack Problem and the greedy approach. Understand the optimal substructure and greedy-choice properties, and learn how to determine the best items to maximize profit within a given weight constraint. Compare t
0 views • 23 slides
Overview of Knapsack Cryptosystems and Related Problems
The Merkle-Hellman knapsack cryptosystem is a cryptographic system that was initially proposed by Merkle, and later iterated versions were both broken by Shamir and Brickell in the early 1980s and 1985, respectively. This system is related to the classical knapsack problem, subset-sum problem, and e
0 views • 18 slides
Impact of Problem Gambling on Poverty and Homelessness
Problem gambling is a significant public health concern leading to financial harm, emotional distress, relationship disruptions, and even homelessness. Men experiencing poverty and homelessness are more susceptible to problem gambling, creating a detrimental cycle. Factors like income level, race, a
0 views • 12 slides
The Importance of Problem-Solving Skills in Everyday Life
Developing effective problem-solving skills is crucial as they play a significant role in various aspects of our daily lives, from simple tasks to complex challenges. This article explores the significance of problem-solving, provides strategies like algorithms and heuristics, discusses obstacles en
0 views • 34 slides
Insights into Polynomials Vanishing on Cartesian Products and the 3POL Problem
This joint work explores polynomials vanishing on Cartesian products, focusing on the 3POL problem involving three sets of points and a 6-variate polynomial. It discusses the running time of solving the explicit 3POL problem and compares it to the well-studied 3SUM problem in theoretical computer sc
0 views • 29 slides
Interesting Graphs and Puzzles for Problem-Solving Enthusiasts
Explore various scenarios involving graph theory and puzzles like handshakes at a party, a tricky river crossing situation with multiple constraints, a jug measuring problem, and the classic Rubik's cube challenge. Also, ponder over a cash exchange problem faced by a group dining at a restaurant. Th
0 views • 8 slides
Solving N-Queen Problem Using Genetic Algorithm
Solving the N-Queen problem involves placing queens on a chessboard in such a way that they cannot check each other. The genetic algorithm approach addresses this problem through representations like phenotype and genotype, fitness evaluation based on queen penalties, mutations involving permutation
0 views • 8 slides
Enhancing Creativity and Problem Solving Techniques
Explore key outcomes in fostering creativity, identifying and removing blocks to problem-solving, and understanding the process of generating new ideas through concepts like creativity vs critical thinking and block-busting. Learn strategies including brainstorming, defer judgment, and morphological
0 views • 15 slides
Enhancing Problem-Solving Skills in Mathematics Workshops
In this workshop focused on problem-solving in mathematics, participants engage in various tasks and activities to develop a deep understanding of problem-solving strategies. The key messages emphasize the importance of integrating problem-solving into daily mathematics learning, utilizing multiple
0 views • 34 slides
Historical Overview of the SLAM Problem
The SLAM problem, a challenging task in mobile robotics, involves creating maps and determining a robot's pose in an unknown environment. Over time, researchers have made significant progress in solving this problem, dating back to the initial probabilistic methods for localization and mapping in 19
0 views • 29 slides
Introduction to Algorithms and Flowcharts
A program consists of instructions given to a computer to execute operations and solve specific problems. To solve a problem in computers, steps like analyzing the problem, writing an algorithm, creating flowcharts, converting flowcharts to programs, and testing the solution must be followed. Algori
1 views • 18 slides
Largest Red-Blue Separating Rectangles Study
This study explores the problem of finding the largest area axis-aligned B-empty rectangle containing n red points and m blue points. The research discusses various extensions to the original problem, such as the Blue Rectangles problem and the Outliers Problem, aiming to achieve efficient solutions
0 views • 20 slides
Problem-Solving Process with Computers
Utilizing computers to solve problems involves various stages such as problem analysis, algorithm development, flowcharting, programming, compilation, debugging, and documentation. It is crucial to plan and understand the problem thoroughly before coding to ensure accurate results. Each step in the
0 views • 55 slides
Solution Circles: A Creative Problem-Solving Tool
Solution Circles is a powerful problem-solving tool that involves a problem presenter, process facilitator, note taker, and brainstorm team. The process includes outlining the problem, brainstorming creative solutions, positive dialogue, and setting achievable first steps within a short timeframe. T
0 views • 10 slides
Best Tree removal Services in Sheldon
If you want the Best Tree removal Services in Sheldon, visit Tree Problem No Problem. Tree Problem No Problem is your local arborist and tree services provider in Thornlands, Queensland. Their specialized experts have been in the trade for more than
1 views • 6 slides