Indirect Proofs: Contradiction and Contraposition Examples
Indirect proofs offer a roundabout approach to proving statements, with argument by contradiction and argument by contraposition being the main techniques. Argument by contradiction involves supposing the statement is false and deriving a contradiction, while argument by contraposition relies on the
3 views • 18 slides
Boolean Logic and Contrapositive Forms in Discrete Math
Delve into the world of Boolean logic and contrapositive forms in discrete math through topics such as simplifications, DeMorgan's Laws, and conditional operators. Explore how to identify equivalent Boolean expressions and prove contrapositive statements using logical reasoning.
0 views • 22 slides
Mathematical Proof Techniques and Examples
Explore various proof techniques in mathematics including direct proofs, proofs by cases, proofs by contrapositive, and examples showing how to prove statements using algebra, definitions, and known results. Dive into proofs involving integers, even and odd numbers, and more to enhance your understa
3 views • 13 slides
Mathematical Proof Methods and Divisibility Rules
In this lesson, we explore various methods of proof in mathematics, including direct proof, contrapositive, proof by contradiction, and proof by cases. We delve into basic definitions of even and odd numbers and learn about proving implications. Additionally, the concept of divisibility, prime numbe
0 views • 30 slides
Discrete Mathematics Learning Goals and Examples in Propositional Logic
Explore the learning goals in discrete mathematics focusing on translating English sentences to propositional logic, evaluating compound propositions, forming converses and contrapositives, and determining consistency. Dive into examples of conditional statements, converse, inverse, contrapositive,
1 views • 14 slides
Propositional Logic Fundamentals
Exploring the key concepts in propositional logic including conditional statements, converse, contrapositive, inverse, biconditionals, logical equivalence, operator precedence, and truth tables. Learn about the importance of truth values and logical equivalences in compound propositions.
0 views • 22 slides
Introduction to Analysis Methods of Proof
This content introduces various methods of proof in analysis, including direct proof, counterexamples, and indirect proofs like contrapositive. It covers common notations, sets, symbols, implications, theorems, and examples with analyses. The goal is to understand how to prove or disprove theorems u
0 views • 22 slides
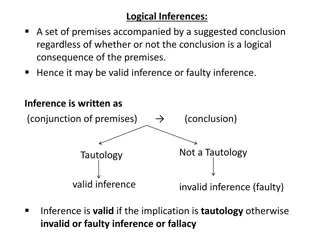
Logical Inferences and Rules of Inference
Logical inferences involve drawing conclusions from premises, which can either be valid or invalid based on the rules of inference. This includes Modus Ponens, Hypothetical Syllogism, DeMorgan's Law, and Law of Contrapositive. Invalid inferences result in fallacies like denying the antecedent. Exerc
0 views • 18 slides
Geometry Standards of Learning Practice Problems
Explore practice problems related to Geometry Standards of Learning (SOL), covering topics such as symbolic representation of arguments, laws of detachment, contrapositive, syllogism, counterexamples, and geometric proofs. Test your understanding of angles, lines, transversals, and congruence to str
0 views • 50 slides
Understanding Logical Laws and Operators in Sets and Logic
Dive into Chapter 2 of "An Experiment: Sets and Logic" to explore logical laws such as DeMorgan's Laws, Commutative, Associative, and Idempotent properties, Tautologies, Contradictions, Conditional Statements, Equivalences, Converse, Contrapositive, Quantifiers, and more in the realm of Sets and Log
1 views • 27 slides
Understanding Conditional Statements and Their Variations
Explore the concept of conditional statements with examples such as if-then statements, converse, inverse, and contrapositive. Learn how to switch, negate, and analyze statements to deepen your understanding of logic and reasoning.
0 views • 7 slides
Proof Techniques: Evenness of 2 and Its Implications - CSE 311 Autumn 2024 Lecture 12
Explore the proofs related to the evenness of the number 2 and its implications, including direct proof, contrapositive, and proof by contradiction. Understand the reasoning behind these techniques through examples and application in mathematical assertions.
0 views • 31 slides
Understanding Propositional Logic: Equivalence and Simplification Examples
Dive into the world of propositional logic with discussions on logical equivalence, distributive property, De Morgan's Law, and truth table simplification. Explore statements, converse, contrapositive, and inverse forms. Learn to express complex statements using quantifiers and logical connectives.
0 views • 9 slides