Computational thinking as 21st Century skill
Computational thinking is a critical skill for the digital age, involving problem-solving techniques that enable computers to process information effectively. It precedes programming and requires breaking down complex problems into manageable steps. Educators emphasize computational thinking exercis
7 views • 4 slides
Master's Program in Computational Drug Discovery and Development - Fall 2024 Curriculum
This Master's program offers a comprehensive curriculum focusing on Artificial Intelligence, Computational Drug Discovery, and Development. With a blend of cutting-edge technologies and practical applications, students delve into techniques, AI/ML, big data mining, modeling, and more. Through intens
1 views • 7 slides
Understanding Computational Linguistics and Natural Language Processing
Explore the fascinating fields of Computational Linguistics and Natural Language Processing (NLP), delving into their development, applications, and significance. Learn about the study of human languages in computational models, the importance of corpora in linguistic research, and the various types
3 views • 33 slides
Understanding the Importance of Pattern Recognition in Computational Thinking
Pattern recognition is a vital skill in computational thinking, enabling the identification of similarities and differences between concepts and objects. By recognizing patterns, individuals can efficiently solve complex problems, create shortcuts, and avoid duplications in problem-solving processes
0 views • 10 slides
Engaging Paper-Based Problem Solving for Computational Thinking Skills
Implementing paper-based problem-solving activities using puzzles, riddles, and pattern recognition can effectively introduce computational thinking without the need for complex technology or terminology. Through real-life scenarios like transporting a fox, chicken, and corn across a river or encodi
0 views • 23 slides
Understanding Complexity in Polynomial Time: MAJORITY-3SAT and Related Problems
Dive into the world of MAJORITY-3SAT and its related problems, exploring the complexity of CNF formulas and the satisfiability of assignments. Discover the intricacies of solving canonical NP-complete problems and the significance of variables in determining computational complexity.
3 views • 35 slides
Computational Thinking, Algorithms & Programming Overview
This unit covers key concepts in computational thinking, including decomposition, abstraction, and algorithmic thinking. Decomposition involves breaking down complex problems, abstraction focuses on identifying essential elements, and algorithmic thinking is about defining clear instructions to solv
1 views • 5 slides
Understanding Computational Complexity Through Statistical Physics
In the age of vast data growth, tackling complex computational problems is crucial. Statistical physics can provide insights into handling the new challenges arising from the exponential increase in data. As we delve into understanding the complexity of computational tasks, it becomes evident that e
0 views • 24 slides
Introduction to Priority Search Trees in Computational Geometry
This lecture outlines the structure and query process of Priority Search Trees (PST) in computational geometry. It covers heap-based point queries, range trees for windowing queries, handling query ranges in 1D and 2D spaces, and using heaps to efficiently handle query ranges. The content discusses
1 views • 18 slides
Computational Complexity and NP-Complete Problems
In today's discussion, we delved into computational complexity and the challenges faced in finding efficient algorithms for various problems. We explored how some problems defy easy categorization and resist polynomial-time solutions. The concept of NP-complete problems was also introduced, highligh
0 views • 38 slides
Ladner's Theorem in Computational Complexity Theory
Ladner's Theorem is a significant result in computational complexity theory that deals with NP-intermediate problems, which are languages in NP neither in P nor NP-complete. The theorem states that if P is not equal to NP, then there must exist an NP-intermediate language. The proof involves a delic
0 views • 48 slides
Insights into Recent Progress on Sampling Problems in Convex Optimization
Recent research highlights advancements in solving sampling problems in convex optimization, exemplified by works by Yin Tat Lee and Santosh Vempala. The complexity of convex problems, such as the Minimum Cost Flow Problem and Submodular Minimization, are being unraveled through innovative formulas
1 views • 47 slides
Introduction to NP-Completeness and Complexity Theory
Explore the concepts of NP-completeness, reductions, and the complexity classes P and NP in computational complexity theory. Learn about decision problems, Boolean functions, languages, polynomial-time Turing machines, and examples of problems in class P. Understand how to deal with functional probl
0 views • 56 slides
Advancing Computational Modeling for National Security and Climate Missions
Irina Tezaur leads the Quantitative Modeling & Analysis Department, focusing on computational modeling and simulation of complex multi-scale, multi-physics problems. Her work benefits DOE nuclear weapons, national security, and climate missions. By employing innovative techniques like model order re
0 views • 6 slides
Insights into Computational Complexity Hierarchy and SAT Algorithms
The computational complexity hierarchy explores classes of problems like EXP-complete, PSPACE-complete, and more. SAT algorithms, such as local search methods and survey propagation, offer new insights into practical complexity. Discover the interplay between tractable and intractable structures in
0 views • 12 slides
Understanding Signatures, Commitments, and Zero-Knowledge in Lattice Problems
Explore the intricacies of lattice problems such as Learning With Errors (LWE) and Short Integer Solution (SIS), and their relation to the Knapsack Problem. Delve into the hardness of these problems and their applications in building secure cryptographic schemes based on polynomial rings and lattice
1 views • 44 slides
Understanding Decision Problems in Polynomial Time Complexity
Decision problems play a crucial role in computational complexity theory, especially in the context of P and NP classes. These problems involve questions with yes or no answers, where the input describes specific instances. By focusing on polynomial-time algorithms, we explore the distinction betwee
0 views • 32 slides
Understanding Computational Biology: Proteins, DNA, RNA, Genetics, and Evolution
Computational Biology combines computational methods with molecular biology to solve biological problems. Explore topics like proteins, DNA, RNA, and genetics, learning about amino acids, nucleotides, and the genetic code. Understand the evolutionary processes of mutation and natural selection.
0 views • 21 slides
Computational Geometry: Algorithms and Methods in Geometric Problem Solving
Explore the realm of computational geometry encompassing line segment crossing, convex hulls, Voronoi diagrams, and element distinctness reduction. Delve into techniques like line crossing checks, enumeration of cross points, and the sweep method, which are crucial for solving geometric problems eff
0 views • 32 slides
Plane Sweep Algorithms in Computational Geometry
Plane sweep algorithms are a powerful technique in computational geometry for solving various problems efficiently. By simulating the sweep of a vertical line across the plane and maintaining a cleanliness property, these algorithms can process events at discrete points in time to update the status
0 views • 26 slides
Understanding Constraint Satisfaction Problems and Search
Constraint Satisfaction Problems (CSPs) involve assigning values to variables while adhering to constraints. CSPs are a special case of generic search problems where the state is defined by variables with possible values, and the goal is a consistent assignment. Map coloring is a classic example ill
0 views • 34 slides
Artificial Intelligence Course at University of South Carolina
This course at University of South Carolina covers topics such as heuristic problem solving, theorem proving, knowledge representation, and reasoning under uncertainty using Bayesian networks. Students will learn to write Prolog programs, formalize computational problems, and apply search algorithms
0 views • 54 slides
Theory of Computation: Decidability and Encoding in CSE 105 Class
Explore the concepts of decidability, encoding, and computational problems in CSE 105 Theory of Computation class. Learn about decision problems, encodings for Turing Machines, framing problems as languages of strings, and examples of computational problems and their encodings. Gain insights into th
0 views • 26 slides
Introduction to Computational Number Theory in Cryptography
Practical private-key cryptography can be done without advanced math, but understanding computational number theory is essential for public-key encryption. This field focuses on the computational difficulty of problems, analyzing algorithms' running times, classifying problems as easy or hard based
0 views • 27 slides
Understanding Computational Problems in Theory of Computation
Today's learning goals in the Theory of Computation class include understanding high-level algorithm descriptions, proving the existence of undecidable languages using counting arguments and diagonalization, and encoding inputs for Turing Machines. Computational problems can be reframed as languages
0 views • 28 slides
Understanding P, NP, NP-Hard, NP-Complete Problems and Amortized Analysis
This comprehensive study covers P, NP, NP-Hard, NP-Complete Problems, and Amortized Analysis, including examples and concepts like Reduction, Vertex Cover, Max-Clique, 3-SAT, and Hamiltonian Cycle. It delves into Polynomial versus Non-Polynomial problems, outlining the difficulties and unsolvability
0 views • 32 slides
Insights into Constraint Satisfaction Problems (CSPs) and Computational Complexity
Delve into the world of Constraint Satisfaction Problems (CSPs) with a focus on Boolean domain instances, computational complexity, testing assignments, and more. Learn about Schaefer's Theorem, query complexities, and characterizing constraint languages. Explore the challenges and optimism in navig
0 views • 19 slides
Understanding the Essence of Computer Science and Computational Thinking
Delve into the fundamentals of Computer Science and Computational Thinking through chapters discussing the nature of science, predictions in physics, and the distinction between Computer Science and Computer Information Systems. Explore the relationships between Math, Physics, and Computer Science i
0 views • 29 slides
Advancing Auditory Enhancement: Integrating Spleeter with Advanced Remixing Techniques in The Cadenza Challenge 2023
Our project for The Cadenza Challenge 2023 focused on improving audio for headphone users with hearing loss by integrating Spleeter's deep learning capabilities. We utilized N-ALR prescriptions, Butterworth bandpass filters, and Dynamic Range Compression to enhance audio quality. By leveraging advan
0 views • 19 slides
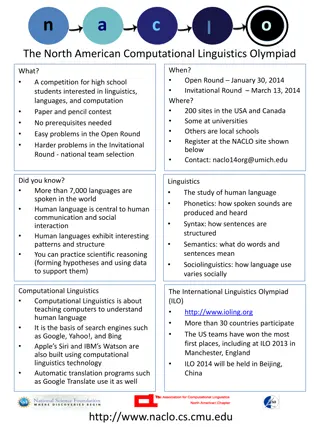
North American Computational Linguistics Olympiad: A Competition for High School Students
The North American Computational Linguistics Olympiad (NACLO) is a competition for high school students interested in linguistics, languages, and computation. It consists of an Open Round in January and an Invitational Round in March, with no prerequisites needed. Participants tackle easy problems i
0 views • 4 slides
Mississippi Center for Supercomputing Research (MCSR) Overview
The Mississippi Center for Supercomputing Research (MCSR) supports computational research in various fields like Chemistry, Bioinformatics, Physics, Engineering, and Computer Science for Mississippi IHLs. They provide training to optimize computational resources, offer classes for computational trai
0 views • 23 slides
Computational Earth Science: Solving Heat Flow in Objects with Complex Shapes Using Finite Difference Method
Explore projects involving the Finite Difference Method for solving static heat conduction problems, also known as the Poisson Equation. Topics include testing boundary conditions, symmetry of solutions, point sources, dipoles, and more. Gain insights into changing boundary conditions and understand
0 views • 20 slides
Theory of Computation Introduction: Dr. Abdulhussein M. Abdullah
Delve into the theory of computation with Dr. Abdulhussein M. Abdullah in the 2nd semester of 2017-2018. Explore the fundamental questions regarding what can be computed, computational problems, and the representation of information. Gain insights into computational models and computability, complex
0 views • 27 slides
Understanding NP-Hard Problems and NP-Completeness
Delve into the complexities of NP-hard problems, NP-complete problems, and the relationships between NP, NP-hard, and NP-complete classes. Learn about easy-to-verify problems in NP, the concept of NP-completeness, the first NP-complete problem - Gates Circuits, and the NP-complete problem CIRCUIT-SA
0 views • 15 slides
Exploring Computational Theories of Brain Function
In this series of images and text snippets, the discussion revolves around the emerging field of computational theories of brain function. Various aspects such as symbolic memories, the relationship between the brain and computation, the emergence of the mind from the brain, and computational thinki
0 views • 53 slides
Computational Earth Science Course Overview
Explore the world of Computational Earth Science with Bill Menke as the instructor and Emily Glazer as the teaching assistant. The course aims to help you become proficient in applying Python-based computational methods to understand dynamic Earth Science phenomena. Through modeling, you will gain i
0 views • 34 slides
Overview of Numerical Methods in Computational Fluid Dynamics
This material delves into the properties, discretization methods, application in PDEs, grid considerations, linear equations solution, and more involved in Numerical Methods in Computational Fluid Dynamics. It covers approaches to fluid dynamical problems, components of numerical methods, and their
0 views • 40 slides
Understanding Pattern Recognition in Computational Thinking
Pattern recognition in computational thinking involves identifying common elements, interpreting differences, and predicting based on patterns. It helps simplify complex problems by recognizing similarities and characteristics shared among them. Through repetition and algorithmic processes, patterns
0 views • 6 slides
Exploring Computational Play in Early Childhood Education: DLI 2023 Workshop
The workshop at the 8th EAI International Conference on Design, Learning & Innovation (DLI 2023) in Aalborg aims to delve into the application of computational play with mathematics in early childhood education. Through live sessions and discussions, opportunities and challenges in utilizing computa
0 views • 7 slides
Fast and Efficient MPM Solver for Strain Localization Problems
This study presents a fast and efficient Material Point Method (MPM) solver for strain localization problems, introducing the Generalized Interpolation Material Point Method (GIMPM) and Convected Particle Domain Interpolation (CPDI). The MPM computational phase involves mapping, nodal solution, and
0 views • 19 slides