Exploring Complexity and Complicatedness in Travel Demand Modeling Systems
Delve into the intricate world of travel demand modeling systems, where complexity arises from dynamic feedback, stochastic effects, uncertainty, and system structure. Discover the balance needed to minimize complicatedness while maximizing behavioral complexity in regional travel modeling. Uncover
0 views • 42 slides
Understanding Time Complexity in Algorithm Analysis
Explore the concept of time complexity in algorithm analysis, focusing on the efficiency of algorithms measured in terms of execution time and memory usage. Learn about different complexities such as constant time, linear, logarithmic, and exponential, as well as the importance of time complexity co
0 views • 73 slides
Understanding Complexity in Polynomial Time: MAJORITY-3SAT and Related Problems
Dive into the world of MAJORITY-3SAT and its related problems, exploring the complexity of CNF formulas and the satisfiability of assignments. Discover the intricacies of solving canonical NP-complete problems and the significance of variables in determining computational complexity.
3 views • 35 slides
Sorting Techniques: Complexity, Stability, and Cases
This content discusses various sorting techniques, their time complexity in worst, best, and average cases, stability, and types of sorts. It includes a comparison table listing algorithms such as Bubble Sort, Selection Sort, Insertion Sort, Quick Sort, and more, along with their respective complexi
0 views • 10 slides
Exploring Complexity in Computational Theory
Dive into a world of computational complexity and theory with a focus on topics such as NP, P, PH, PSPACE, NL, L, random vs. deterministic algorithms, and the interplay of time and space complexity. Discover insights on lower bounds, randomness, expanders, noise removal, and the intriguing question
0 views • 17 slides
Quantum Query Complexity Measures for Symmetric Functions
Explore the relationships between query complexity measures, including quantum query complexity, adversary bounds, and spectral sensitivity, in the context of symmetric functions. Analysis includes sensitivity graphs, the quantum query model, and approximate counting methods. Results cover spectral
0 views • 19 slides
Understanding Computational Complexity Through Statistical Physics
In the age of vast data growth, tackling complex computational problems is crucial. Statistical physics can provide insights into handling the new challenges arising from the exponential increase in data. As we delve into understanding the complexity of computational tasks, it becomes evident that e
0 views • 24 slides
Exploring Proof Complexity: The Basics, Achievements, and Challenges
Delve into the intricacies of proof complexity, covering propositional, algebraic, and semi-algebraic proof systems, lower bound methods, and algorithmic implications. Discover fundamental connections to complexity theory and open problems in the field.
0 views • 76 slides
Developing Effective Reading Work Samples
Creating reading work samples involves steps like identifying a topic, analyzing passages, drafting tasks, formatting, administering, scoring, and revising tasks. Considerations include text complexity, high student interest, and grade-level appropriateness. Text complexity is assessed quantitativel
0 views • 15 slides
Understanding Computational Complexity in Quantum Hamiltonians
The Bose-Hubbard model is proven to be QMA-complete, indicating the challenge in solving ground energy problems in quantum systems. Various classes of Hamiltonians, such as k-local and stoquastic, exhibit different complexities in computing ground energy. While some systems with QMA-complete ground
0 views • 40 slides
Additive Combinatorics Approach to Log-Rank Conjecture in Communication Complexity
This research explores an additive combinatorics approach to the log-rank conjecture in communication complexity, addressing the maximum total bits sent on worst-case inputs and known bounds. It discusses the Polynomial Freiman-Ruzsa Conjecture and Approximate Duality, highlighting technical contrib
0 views • 9 slides
Overview of Computational Complexity Theory: Savitch's Theorem, PSPACE, and NL-Completeness
This lecture delves into Savitch's theorem, the complexity classes PSPACE and NL, and their completeness. It explores the relationship between time and space complexity, configuration graphs of Turing machines, and how non-deterministic space relates to deterministic time. The concept of configurati
0 views • 67 slides
Computational Complexity and NP-Complete Problems
In today's discussion, we delved into computational complexity and the challenges faced in finding efficient algorithms for various problems. We explored how some problems defy easy categorization and resist polynomial-time solutions. The concept of NP-complete problems was also introduced, highligh
0 views • 38 slides
Exploring Circuit Size Bounds in Complexity Theory
The article delves into Shannon's Theorem in Complexity Theory, discussing the upper bounds of circuit sizes for Boolean functions of n variables. It explores the 1-1 correspondence with 0-1 strings of length 2n and how Boolean functions can be expressed as CNF or DNF formulas. The computation of th
2 views • 19 slides
Achieving Sublinear Complexity in Dynamic Networks
This research explores achieving sublinear complexity under constant ? in dynamic networks with ?-interval updates. It covers aspects like network settings, communication models, fundamental problems considered, existing results, and challenges in reducing complexity. The focus is on count time comp
0 views • 14 slides
Enhancing Spectrum Efficiency with Low Complexity Erasure Codes in IEEE 802.11 Document
This document delves into the implementation of erasure codes for content channels in IEEE 802.11 systems. By utilizing erasure codes, spectrum efficiency can be boosted without significantly increasing the complexity of encoding and decoding processes. The discussion also covers the duplication of
0 views • 20 slides
Introduction to NP-Completeness and Complexity Theory
Explore the concepts of NP-completeness, reductions, and the complexity classes P and NP in computational complexity theory. Learn about decision problems, Boolean functions, languages, polynomial-time Turing machines, and examples of problems in class P. Understand how to deal with functional probl
0 views • 56 slides
Insights into Computational Complexity Hierarchy and SAT Algorithms
The computational complexity hierarchy explores classes of problems like EXP-complete, PSPACE-complete, and more. SAT algorithms, such as local search methods and survey propagation, offer new insights into practical complexity. Discover the interplay between tractable and intractable structures in
0 views • 12 slides
Understanding Complexity Theory in C++
Delve into the world of Complexity Theory with Cynthia Bailey Lee's peer instruction materials on P/NP definitions, decision vs. optimization problems, and the concept of O(2^n) time complexity. Explore the distinctions between problems in P and NP sets, grasp the implications of problem-solving spe
0 views • 27 slides
Understanding Signatures, Commitments, and Zero-Knowledge in Lattice Problems
Explore the intricacies of lattice problems such as Learning With Errors (LWE) and Short Integer Solution (SIS), and their relation to the Knapsack Problem. Delve into the hardness of these problems and their applications in building secure cryptographic schemes based on polynomial rings and lattice
0 views • 44 slides
Understanding Decision Problems in Polynomial Time Complexity
Decision problems play a crucial role in computational complexity theory, especially in the context of P and NP classes. These problems involve questions with yes or no answers, where the input describes specific instances. By focusing on polynomial-time algorithms, we explore the distinction betwee
0 views • 32 slides
Understanding Optimization Problems in Complexity Theory
Exploring optimization problems in complexity theory, which involve finding the best solution rather than a simple yes/no answer. These NP-hard problems require close-to-optimal results as exact solutions are likely intractable. Section 10.1 of the textbook and Papadimitriou's book provide insights
0 views • 13 slides
Understanding Text Complexity in Science and Literacy Education
Exploring the concept of text complexity beyond the familiar realm of Oz, this presentation delves into quantitative and qualitative measures, reader and task considerations, and steps to assess text complexity. Various resources and examples are provided to help educators gauge and improve the comp
0 views • 43 slides
Holographic Complexity in Hybrid De Sitter Spacetime
The research delves into holographic complexity in a hybrid de Sitter spacetime, exploring the AdS/CFT correspondence, quantum information in the bulk, and computational complexity. It also examines the volume of the ERB, evolution of complexity in CFT, and probes cosmological horizons using hologra
0 views • 12 slides
Understanding Cook-Levin Theorem in NP-Completeness
The Cook-Levin theorem establishes the NP-completeness of the SAT language by showing how every problem in NP can be reduced to SAT. It demonstrates that computation is a local process where each step only affects a constant number of bits. Through this, a polynomial time computable function can be
0 views • 84 slides
Insights into NP-Hard Problems in Molecular Biology and Genetics
Understanding the complexity of NP-Hard Problems arising in molecular biology and genetics is crucial. These problems involve genome sequencing, global alignment of multiple genomes, identifying relations through genome comparison, discovering dysregulated pathways in human diseases, and finding spe
0 views • 24 slides
Understanding P, NP, NP-Hard, NP-Complete Problems and Amortized Analysis
This comprehensive study covers P, NP, NP-Hard, NP-Complete Problems, and Amortized Analysis, including examples and concepts like Reduction, Vertex Cover, Max-Clique, 3-SAT, and Hamiltonian Cycle. It delves into Polynomial versus Non-Polynomial problems, outlining the difficulties and unsolvability
0 views • 32 slides
Understanding Decision Problems in P and NP Complexity Classes
Decision problems play a crucial role in the realm of computational complexity theory, defining questions with binary answers that form the basis of the P and NP classes. This article delves into the significance of polynomial-time algorithms, distinguishes between tractable and intractable problems
0 views • 32 slides
Insights into Constraint Satisfaction Problems (CSPs) and Computational Complexity
Delve into the world of Constraint Satisfaction Problems (CSPs) with a focus on Boolean domain instances, computational complexity, testing assignments, and more. Learn about Schaefer's Theorem, query complexities, and characterizing constraint languages. Explore the challenges and optimism in navig
0 views • 19 slides
Understanding NP-Hard Problems and NP-Completeness
Delve into the complexities of NP-hard problems, NP-complete problems, and the relationships between NP, NP-hard, and NP-complete classes. Learn about easy-to-verify problems in NP, the concept of NP-completeness, the first NP-complete problem - Gates Circuits, and the NP-complete problem CIRCUIT-SA
0 views • 15 slides
Understanding Complexity Measures of Boolean Functions
This work delves into the intricate world of complexity measures for Boolean functions, exploring concepts such as certificate complexity, decision tree depth, sensitivity, block sensitivity, PRAM complexity, and more. It sheds light on the relationships among different complexity measures and provi
0 views • 36 slides
Improved Merlin-Arthur Protocols for Fine-Grained Complexity Problems
The text discusses Merlin-Arthur proof systems and protocols for central problems in fine-grained complexity, particularly focusing on the time complexity, completeness, and soundness of these protocols. It also touches on recent interest in these protocols and presents new results in areas such as
0 views • 16 slides
Interactive Proofs in Complexity Theory
Delve into the realm of interactive proofs in complexity theory, exploring concepts such as completeness, soundness, and efficiency. Discover how interactive proof systems can be utilized in scenarios like graph isomorphism and their implications on the complexity classes NP and coNP. Uncover the in
0 views • 40 slides
Understanding QMA(2): Hamiltonians, Provers, and Complexity Classes
Exploring the complexities of QMA(2) through discussions on separable sparse Hamiltonians, the power of Merlin in L.QMA, the impact of prover restrictions on complexity classes like IP and MIP, and the difference between Merlin.A, Merlin.B, and Arthur in L.QMA(2). Delve into short proofs for NP-Comp
0 views • 27 slides
Challenges in Software Development: Understanding the Complexity
Society's dependence on software is increasing, yet many major software projects fail due to factors like late delivery, budget overruns, and changing requirements. Development challenges arise from the inherent complexity of software systems, human factors, and the need for creativity in solving ne
0 views • 30 slides
Orthogonal Vectors Conjecture and Sparse Graph Properties Workshop
Exploring the computational complexity of low-polynomial-time problems, this workshop delves into the Orthogonal Vectors Problem and its conjectures. It introduces concepts like the Sparse OV Problem, first-order graph properties, and model checking in graphs. Discussing the hardness of problems rel
2 views • 22 slides
Understanding PSPACE-Complete Problems in Complexity Theory
This content delves into complexity theory, exploring PSPACE-complete problems and their relevance within the realm of theoretical computer science. It covers concepts such as time complexity classes, P vs. NP dilemma, NP-complete languages, space complexity, PSPACE vs. NPSPACE, and PSPACE completen
1 views • 19 slides
Understanding NP-Complete Problems and Reductions
Exploring the realm of complexity theory, this topic delves into NP-complete problems and various types of reductions. From the Cook-Levin Theorem to the P vs. NP question, it navigates through the intricacies of computational complexity, time complexity classes, and the concept of reducibility in r
0 views • 38 slides
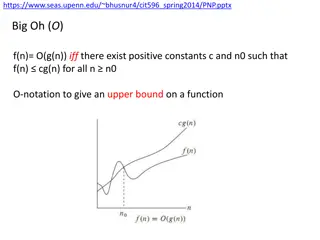
Understanding Big O Notation and Problem Complexity
Big O notation, Omega notation, and Theta notation are used in algorithm analysis to describe upper and lower bounds on functions. They help determine the efficiency and complexity of algorithms in terms of time and space. The content also covers examples of common computational problems like sortin
0 views • 39 slides
Quantum Space-Bounded Complexity in Logarithmic Space: A Comprehensive Overview
Quantum space-bounded complexity explores the memory requirements for solving problems in log space. Examples include matrix multiplication, undirected graph connectivity, and problems like inverting matrices and determining connectivity. The significance of deterministic log space (NL) and nondeter
0 views • 49 slides