Principles and Applications of Symmetry in Magnetism Summer School Lecture
This lecture delves into the principles and applications of symmetry in magnetism, covering topics such as the symmetry of response tensors, transformations of tensors, time-reversal symmetry, and beyond point groups. It explores the symmetry of local effects, equivalent magnetic configurations, exp
3 views • 14 slides
Electrical Field Theory: Vector Analysis in Different Coordinate Systems
Explore the principles of Vector Analysis in Cartesian, Cylindrical, and Spherical coordinate systems as applied to Electrical Field Theory. Learn how to calculate differential lengths, areas, and volumes, and solve practical examples under the guidance of Prof. Dr. Ahmed Mohamed El-Sawy.
5 views • 10 slides
Introduction to Cartesian Components of Vectors in Two-Dimensional Space
Exploring Cartesian components of vectors in a two-dimensional coordinate frame using unit vectors i and j. Learn how to express vectors, add them using the triangle law, use column vector notation, and find resultant vectors. Understand position vectors in terms of coordinates. Examples and diagram
0 views • 16 slides
3D Transformations in Computer Graphics
Transformation plays a crucial role in computer graphics, enabling movement and manipulation of objects in a Cartesian plane. This comprehensive guide covers types of transformations, reasons for using them, and details on 3D translation, rotation, scaling, reflection, and shearing. Explore the sign
2 views • 25 slides
Graphs: An Introduction to Data Visualization
This chapter delves into various types of graphs used in data representation, such as bar graphs, pie graphs, histograms, line graphs, and linear graphs. It explains the purpose and structure of each graph type, along with practical examples. Additionally, it covers the Cartesian system for locating
0 views • 15 slides
Functions and Graphs in Mathematics
Functions are a fundamental concept in mathematics used to describe relationships in the real world. They can be represented through equations, graphs, tables, or verbal descriptions. A function maps elements from a domain to a range, where each input has a unique output. The domain encompasses all
0 views • 4 slides
Coordinate Geometry in Mathematics
Coordinate geometry, a system developed in 1637 by Descartes and Fermat, allows for locating points in a Cartesian plane using x and y coordinates. This concept involves recalling coordinate axes, plotting points, understanding quadrants, and solving real-life problems. The history, introduction, an
3 views • 27 slides
Computer Graphics: Evolution and Applications
Computer graphics represent the creation and manipulation of visual information using specialized hardware and software. This field has evolved since the 1950s, enabling diverse applications like entertainment, CAD, education, e-commerce, and computer art. The origins date back to MIT's early displa
1 views • 22 slides
Comprehensive Guide to CNC Part Programming
Learn about CNC part programming for turning and milling machines. Understand the importance of part programs, program input devices, machine control unit functions, and CNC programming methods like offline and conversational programming. Explore the Cartesian coordinate system, tool positioning, an
0 views • 61 slides
2D Viewing in Computer Graphics
Exploring the concept of 2D viewing in computer graphics, this lecture covers the 2D viewing pipeline, including clipping, window normalization, viewport transformations, and OpenGL 2D viewing functions. It explains how a picture is defined using a Cartesian coordinate system, selecting views within
3 views • 84 slides
Mathematicians Through Time: Pioneers in Mathematics
Delve into the lives and contributions of influential mathematicians throughout history, from Pythagoras and Euclid to Archimedes, Fibonacci, Descartes, and Isaac Newton. Learn about their groundbreaking discoveries, from the Pythagorean theorem to the Fibonacci sequence and the Cartesian plane, sha
8 views • 10 slides
Explore the Scientific Revolution
The Scientific Revolution marked a shift from the medieval worldview to a secular, rational, and materialistic perspective. Key terms such as geocentric and heliocentric conceptions, Cartesian dualism, rationalism, and the scientific method played pivotal roles in shaping this transformative period.
7 views • 10 slides
René Descartes: Philosopher and Mathematician Extraordinaire
René Descartes, known as the Father of Modern Philosophy, made significant contributions to both philosophy and mathematics. Born in 1596 in France, Descartes received a Jesuit education and later worked as a Corps of Engineers applying mathematics to practical applications. His philosophical works
0 views • 15 slides
Interactive Design Workshop: Pine Tree Creation Using Design Thinking
Join us in an engaging design workshop where you will learn the principles of Design Thinking by drawing a pine tree on a Cartesian plane. Through activities like warming up, empathizing, ideating, defining, and prototyping, you will enhance your collaborative problem-solving skills while creating i
0 views • 14 slides
Linear Algebra Applications in Neutrino Experiments
Linear Algebra plays a crucial role in various neutrino experiments, enabling solutions in weighted least squares, energy estimation in EXO-200, and signal processing in LArTPC detectors. From Cartesian coordinates to minimizing uncertainties, linear algebra techniques contribute significantly to da
0 views • 38 slides
Efficient Virtual Segmentation for Large-scale Detector Systems
Highly segmented detectors with millions to billions of readout channels require a practical approach for simulation and reconstruction. Implementing each channel separately is impractical, necessitating the use of virtual segmentation to define readouts for different detector components. Dependenci
0 views • 11 slides
Peer Instruction in Discrete Mathematics
Explore topics in discrete mathematics such as set sizes, set builder notation, power sets, Cartesian products, unions, intersections, and different ways of defining sets. Learn through engaging visuals and examples presented under a Creative Commons License by Dr. Cynthia Bailey Lee and Dr. Shachar
0 views • 16 slides
PowerGrid: Reconstructing High-Resolution Non-Cartesian MRI Data for Bioengineering Research
PowerGrid is a cutting-edge system developed by Brad Sutton, Assoc. Prof. at the University of Illinois, for harnessing high-performance computing to reconstruct large sets of high-resolution non-Cartesian MRI data. This technology addresses the need for improved image reconstruction packages in MRI
0 views • 10 slides
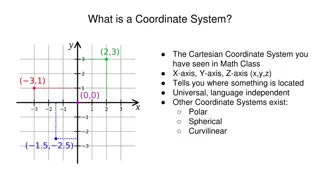
Coordinate Systems in Mathematics and Astronomy
Coordinate systems such as Cartesian, Polar, and Celestial serve as frameworks for locating points in space. They include dimensions like x, y, z axes in Cartesian, Latitude and Longitude on Earth, and various systems for astronomical observations. Different coordinate systems cater to specific purp
0 views • 11 slides
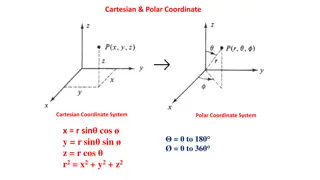
Cartesian and Polar Coordinate Systems
Explore the concepts of Cartesian and Polar coordinate systems, including their formulas and visual representations. Dive into the relationships between Cartesian and Polar coordinates, as well as their applications in mathematics and physics. Discover orbital shapes such as Px, Py, Pz, and dz2 orbi
0 views • 12 slides
Insights into Polynomials Vanishing on Cartesian Products and the 3POL Problem
This joint work explores polynomials vanishing on Cartesian products, focusing on the 3POL problem involving three sets of points and a 6-variate polynomial. It discusses the running time of solving the explicit 3POL problem and compares it to the well-studied 3SUM problem in theoretical computer sc
0 views • 29 slides
Mathematical Discoveries at PMEG 2023
Explore the world of math through workshops, activities, and project presentations at PMEG 2023. Dive into Euclidean Geometry, straight lines, Monopoly, Fibonacci, Cartesian Planes, linear equations, and binary code with our dynamic teams. Unveil the possibilities of mathematical exploration!
0 views • 5 slides
Creating a CMS Simulation: Grid Domain Activity Dataset Development
Developing a CMS simulation involves loading bathymetry data, setting boundary conditions, creating grid domains (land/water), and choosing between Quadtree or Cartesian grid structures. Learn how to manage survey datasets, add new coverages, define grid frames, and set up the land/water interface f
0 views • 14 slides
Analytical Solutions for 2D Heat Equation with Separation of Variables
Consider the steady-state 2D heat equation with constant thermal conductivity. Analyze analytical solutions using separation of variables method for a square plate with defined boundary conditions. Learn how to express the general form of solutions and apply them to the heat equation in Cartesian ge
0 views • 15 slides
Efficient Hardware Architectures for Deep Neural Network Processing
Discover new hardware architectures designed for efficient deep neural network processing, including SCNN accelerators for compressed-sparse Convolutional Neural Networks. Learn about convolution operations, memory size versus access energy, dataflow decisions for reuse, and Planar Tiled-Input Stati
0 views • 23 slides
Materialist Theories of the Self: Diderot's Perspective
Materialism, as explored by Diderot and other philosophers, delves into the intricate relationship between mind and matter. Diderot questions the nature of the self and challenges Cartesian anti-materialist views. He considers the self as an organic unity, emphasizing the interplay of external relat
0 views • 11 slides
Vector Calculus II Concepts with Examples by Prof. Somesh Kr. Malhotra
Explore advanced topics in vector calculus including gradient, divergence, curl, and theorems like the Divergence Theorem and Stokes' Theorem. Follow along with examples presented in Cartesian, spherical, and cylindrical coordinates to deepen your understanding of vector calculus concepts.
0 views • 29 slides
Classification and Application of Robotic Systems
Robots can be classified based on configuration, control system type, sequence variability, and controlling method. Kinematic structures further categorize robots into Cartesian, Cylindrical, Spherical, SCARA, and Revolute types. Each type has specific applications, uses, advantages, and disadvantag
0 views • 14 slides
MultiD Quadratures: Strategies and Solutions
Explore the concept of multidimensional discrete ordinates and quadratures in Cartesian coordinates, along with differences in solution strategies. Learn about the octants in unit directional sphere and the relationships between geometries and octants. Discover how to handle directional flux depende
0 views • 27 slides
Graphics Output Primitives and Coordinate Reference Frames
Graphics output primitives and coordinate reference frames play a crucial role in describing scenes and drawing basic geometric structures in 2D space. These concepts involve defining points, drawing lines, and understanding pixel coordinates within a coordinate system. Absolute and relative coordin
3 views • 35 slides
Counting Principles in Discrete Structures
Counting serves a crucial role in algorithm design and complexity analysis, enabling us to determine program time and space complexities. This article explores counting principles such as the sum and product rules, Cartesian products, and their applications in solving simple and complex counting pro
0 views • 33 slides
Sets and Functions in Discrete Structures
Sets are unordered collections of objects in mathematics, with elements or members that can belong to multiple well-known sets such as integers, real numbers, and more. Set builders help define elements within a set, while subsets and the power set play essential roles in set theory. The concept of
0 views • 44 slides
Deformation and Strain in Engineering
Deformation occurs when a force is applied to a body, causing changes in its shape and size. Normal strain refers to the elongation or contraction of a line segment per unit length, while shear strain is the change in angle between two originally perpendicular line segments. Cartesian strain compone
0 views • 6 slides