Algorithm Analysis
Algorithm analysis involves evaluating the efficiency of algorithms through measures such as time and memory complexity. This analysis helps in comparing different algorithms, understanding how time scales with input size, and predicting performance as input size approaches infinity. Scaling analysi
1 views • 30 slides
Clinical Algorithm for Rash Evaluation
The clinical algorithm outlines the evaluation process for a patient presenting with a rash, focusing on the assessment for measles transmission. It covers key criteria, testing recommendations, and guidelines for suspected measles cases. Healthcare providers can utilize this algorithm to determine
0 views • 5 slides
Understanding Booth's Algorithm for Binary Integer Division
Learn about Booth's Algorithm and how it facilitates binary integer division. Discover key points to remember when using the algorithm, steps to initiate the process, and a detailed example to illustrate the multiplication of two operands using Booth's Algorithm.
0 views • 42 slides
Understanding Stable Matchings and the Gale-Shapley Algorithm
The concept of stable matchings is explored, along with the Gale-Shapley algorithm for finding them efficiently. Key ideas and steps of the algorithm are explained, supported by visuals. The process, examples, and observations related to the algorithm's effectiveness are discussed, highlighting the
1 views • 29 slides
Understanding Time Complexity in Algorithm Analysis
Explore the concept of time complexity in algorithm analysis, focusing on the efficiency of algorithms measured in terms of execution time and memory usage. Learn about different complexities such as constant time, linear, logarithmic, and exponential, as well as the importance of time complexity co
0 views • 73 slides
Ricart and Agrawala's Algorithm for Mutual Exclusion
The Ricart-Agrawala Algorithm is a distributed system algorithm for achieving mutual exclusion without the need for release messages, developed by Glenn Ricart and Ashok Agrawala. The algorithm involves processes sending timestamped requests to enter a critical section, with careful handling of repl
1 views • 16 slides
Understanding Algorithm Efficiency Analysis
In this chapter, Dr. Maram Bani Younes delves into the analysis of algorithm efficiency, focusing on aspects such as order of growth, best case scenarios, and empirical analysis of time efficiency. The dimensions of generality, simplicity, time efficiency, and space efficiency are explored, with a d
1 views • 28 slides
Understanding Lamport Algorithm for Mutual Exclusion
Lamport Algorithm, presented by Prafulla Santosh Patil, is a permission-based algorithm utilizing timestamps to order critical section requests and resolve conflicts. It employs three types of messages: REQUEST, REPLY, and RELEASE, where each site manages a queue to store requests. By ensuring commu
0 views • 15 slides
Digital Differential Analyzer (DDA) Algorithm in Computer Graphics
In computer graphics, the Digital Differential Analyzer (DDA) Algorithm is utilized as the basic line drawing algorithm. This method involves interpolation of variables between two endpoints to rasterize lines, triangles, and polygons efficiently. The algorithm requires inputting coordinates of two
0 views • 9 slides
Understanding Diffie-Hellman Key Exchange Algorithm
The Diffie-Hellman key exchange algorithm, a pioneering public-key cryptography method introduced by Diffie and Hellman in 1976, enables secure key exchange between two users to facilitate subsequent message encryption. The algorithm relies on the complexity of computing discrete logarithms and invo
0 views • 24 slides
Efficient Line Segment Intersection Algorithm
This content discusses the Line Segment Intersection problem and presents an efficient algorithm using the line sweep technique. The algorithm utilizes ordered sets implemented as balanced search trees to efficiently determine if any two line segments intersect in the plane. By sorting endpoints and
0 views • 10 slides
Quantum Query Complexity Measures for Symmetric Functions
Explore the relationships between query complexity measures, including quantum query complexity, adversary bounds, and spectral sensitivity, in the context of symmetric functions. Analysis includes sensitivity graphs, the quantum query model, and approximate counting methods. Results cover spectral
0 views • 19 slides
Grey Wolf Optimizer: A Nature-Inspired Optimization Algorithm
The Grey Wolf Optimizer algorithm is based on the social hierarchy of grey wolves in the wild. Inspired by the pack behavior of grey wolves, this algorithm utilizes alpha, beta, and delta solutions to guide the optimization process. The hunting phases of tracking, pursuing, and attacking prey mimic
3 views • 16 slides
Emergency Paediatric Tracheostomy Management Algorithm
Emergency Paediatric Tracheostomy Management Algorithm provides a structured approach for managing pediatric patients requiring tracheostomy in emergency situations. The algorithm outlines steps for assessing airway patency, performing suction, and changing the tracheostomy tube if necessary. It emp
0 views • 4 slides
Development of Satellite Passive Microwave Snowfall Detection Algorithm
This study focuses on the development of a satellite passive microwave snowfall detection algorithm, highlighting the challenges in accurately determining snowfall using satellite instruments. The algorithm uses data from AMSU/MHS, ATMS, and SSMIS sensors to generate snowfall rate estimates, overcom
0 views • 20 slides
Achieving Sublinear Complexity in Dynamic Networks
This research explores achieving sublinear complexity under constant ? in dynamic networks with ?-interval updates. It covers aspects like network settings, communication models, fundamental problems considered, existing results, and challenges in reducing complexity. The focus is on count time comp
0 views • 14 slides
Understanding Euclid's Algorithm: An Ancient Approach to Finding Greatest Common Divisors
Euclid's Algorithm, dating back 2500 years, offers a simpler method to find the greatest common divisor (gcd) of two non-negative integers compared to traditional factorization. By iteratively applying a rule based on the gcd of remainders, it efficiently computes gcd values. The basis of the algori
0 views • 15 slides
Understanding Complexity in Data Structures
Introduction to logarithms, fractional exponents, and complexity analysis in algorithms. Exploring Big O notation to express algorithm complexity and examples demonstrating different time complexities. Learn about the importance of analyzing the efficiency of algorithms in data structures.
0 views • 79 slides
Understanding Algorithm Analysis: Key Concepts and Methods
Explore algorithm analysis principles including input size characterization, order of growth evaluation, and intractability of problems. Learn how algorithms are compared based on resource utilization and discover the significance of time complexity in algorithm performance assessment.
0 views • 25 slides
GPU Accelerated Algorithm for 3D Delaunay Triangulation
Thanh-Tung Cao, Todd Mingcen Gao, Tiow-Seng Tan, and Ashwin Nanjappa from the National University of Singapore's Bioinformatics Institute present a GPU-accelerated algorithm for 3D Delaunay triangulation. Their work explores the background, related works, algorithm implementation, and results of thi
0 views • 24 slides
Introduction to QuickSort Algorithm
Explore the QuickSort algorithm with details on the worst-case time complexity, partitioning process, recursive method, and example scenarios. Understand how QuickSort efficiently sorts arrays by choosing a pivot, comparing elements, and recursively partitioning the array until sorted. Dive into the
0 views • 19 slides
Cuckoo Search: A Nature-Inspired Optimization Algorithm
Cuckoo Search (CS) algorithm, developed in 2009, mimics the brood parasitism of cuckoo species and utilizes Lévy flights for efficient optimization. This algorithm has shown promise in outperforming other traditional methods like PSO and genetic algorithms. The behavior of cuckoos in laying eggs an
0 views • 25 slides
Understanding Big-Oh Notation in Time Complexity Analysis
Big-Oh notation in algorithm analysis signifies how the runtime of an algorithm grows in relation to the input size. It abstractly characterizes the worst-case time complexity, disregarding constants and lower-order terms. The concept of Big-Oh, along with Big-Omega and Big-Theta, helps in comparing
0 views • 18 slides
Ford-Fulkerson Algorithm for Maximum Flow in Networks
The Ford-Fulkerson algorithm is used to find the maximum flow in a network by iteratively pushing flow along paths and updating residual capacities until no more augmenting paths are found. This algorithm is crucial for solving flow network problems, such as finding min-cuts and max-flow. By modelin
0 views • 26 slides
3GPP Voting Rights Algorithm: Contiguous-3 Solution Evaluation
This evaluation delves into the advantages and disadvantages of the 3 Contiguous-3 solution within the 3GPP voting rights algorithm. It explores scenarios to test the algorithm's effectiveness in granting and revoking voting rights based on meeting attendance types. The evaluation includes diverse h
0 views • 10 slides
Introduction to Algorithm Analysis and Complexity in Computer Science
Algorithm analysis is crucial in determining the efficiency of programs by analyzing resource usage such as time and space. This involves comparing programs, understanding data structures, and evaluating algorithm performance. Efficiency is key as program execution time depends on various factors be
0 views • 66 slides
Bresenham Line Drawing Algorithm Explained with Examples
Bresenham Line Drawing Algorithm is a method used to generate points between starting and ending coordinates to draw lines efficiently. This algorithm involves calculating parameters, decision parameters, and iteratively finding points along the line. Two example problems are provided with step-by-s
0 views • 8 slides
Algorithm Strategies: Greedy Algorithms and the Coin-changing Problem
This topic delves into general algorithm strategies, focusing on the concept of greedy algorithms where locally optimal choices are made with the hope of finding a globally optimal solution. The discussion includes the nature of greedy algorithms, examples such as Dijkstra's algorithm and Prim's alg
0 views • 91 slides
Understanding Algorithm Efficiency and Complexity
Exploring the importance of simplicity, efficiency, and correctness in algorithms. Learn about basic steps, counting steps, and operations that affect algorithm speed. Discover key factors in determining algorithm superiority. Dive into the world of algorithmic efficiency without compromising on fun
0 views • 35 slides
Understanding Bubble Sort Algorithm - COEN 352 by Tawfiq Jawhar
Dive into the world of sorting algorithms with a focus on Bubble Sort. Explore how Bubble Sort works through animations, visual representations, and explanations of its time complexity, stability, and in-place nature. Discover the significance of one iteration in Bubble Sort and how it affects the a
0 views • 17 slides
Stable Matching Problem and Gale-Shapley Algorithm Overview
The content provides information on the stable matching problem and the Gale-Shapley algorithm. It covers the definition of stable matching, the workings of the Gale-Shapley algorithm, tips for algorithm implementation, and common questions related to the topic. The content also includes a summary o
0 views • 16 slides
Understanding Text Complexity in Science and Literacy Education
Exploring the concept of text complexity beyond the familiar realm of Oz, this presentation delves into quantitative and qualitative measures, reader and task considerations, and steps to assess text complexity. Various resources and examples are provided to help educators gauge and improve the comp
0 views • 43 slides
Holographic Complexity in Hybrid De Sitter Spacetime
The research delves into holographic complexity in a hybrid de Sitter spacetime, exploring the AdS/CFT correspondence, quantum information in the bulk, and computational complexity. It also examines the volume of the ERB, evolution of complexity in CFT, and probes cosmological horizons using hologra
0 views • 12 slides
Understanding Deutsch's Algorithm in Quantum Computing
Deutsch's Algorithm is a fundamental quantum algorithm designed to solve the problem of determining if a given function is constant or balanced. This algorithm leverages quantum principles such as superposition and entanglement to provide a more efficient solution compared to classical methods. By e
0 views • 17 slides
Algorithm for Determining Endpoints in Speech Recognition
This article discusses an algorithm proposed by L.R. Rabiner and M.R. Sambur in 1975 for determining endpoints in isolated utterances. The algorithm focuses on detecting word boundaries in speech through the recognition of silence, which can lead to reduced processing load and increased convenience,
0 views • 22 slides
Understanding Complexity Measures of Boolean Functions
This work delves into the intricate world of complexity measures for Boolean functions, exploring concepts such as certificate complexity, decision tree depth, sensitivity, block sensitivity, PRAM complexity, and more. It sheds light on the relationships among different complexity measures and provi
0 views • 36 slides
Time-space Tradeoffs and Optimizations in BKW Algorithm
Time-space tradeoffs and optimizations play a crucial role in the BKW algorithm, particularly in scenarios like learning parity with noise (LPN) and BKW algorithm iterations. The non-heuristic approach in addressing these tradeoffs is discussed in relation to the hardness of the LPN problem and the
0 views • 14 slides
Interactive Proofs in Complexity Theory
Delve into the realm of interactive proofs in complexity theory, exploring concepts such as completeness, soundness, and efficiency. Discover how interactive proof systems can be utilized in scenarios like graph isomorphism and their implications on the complexity classes NP and coNP. Uncover the in
0 views • 40 slides
Understanding PSPACE-Complete Problems in Complexity Theory
This content delves into complexity theory, exploring PSPACE-complete problems and their relevance within the realm of theoretical computer science. It covers concepts such as time complexity classes, P vs. NP dilemma, NP-complete languages, space complexity, PSPACE vs. NPSPACE, and PSPACE completen
1 views • 19 slides
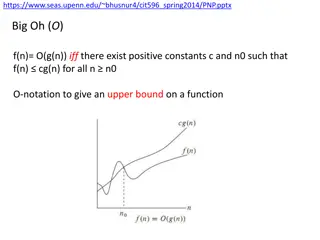
Understanding Big O Notation and Problem Complexity
Big O notation, Omega notation, and Theta notation are used in algorithm analysis to describe upper and lower bounds on functions. They help determine the efficiency and complexity of algorithms in terms of time and space. The content also covers examples of common computational problems like sortin
0 views • 39 slides