Understanding Inclined Planes and Friction Forces
Introduction to inclined planes, components of forces, dealing with friction on whiteboards, and demonstrations on block forces on inclined planes. Learn about calculating components of gravity, friction forces, and scenarios involving kinetic and static friction on an inclined plane.
Uploaded on May 14, 2024 | 3 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Inclined Planes Introduction Components Normal Force Whiteboards (No friction) Dealing with friction Whiteboards (With friction) Demo - inclined plane/block mg
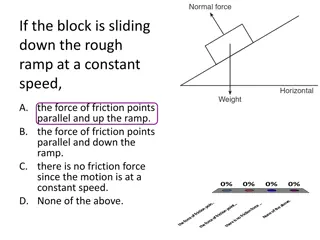
Consider an object on an inclined plane: Gravity is down But things happen along the plane So we make components of gravity mg
Meet the components - they are your friends! Fperp - perpendicular to the plane mg F|| - parallel to the plane
R = mgcos (reaction force) And the plane pushes back (It doesn t break) Fperp = mgcos mg Since we know the angle, we can calculate the components F|| = mgsin (Acts down the plane)
21.502 15.430 22.925 26.0o A 5.00 kg object is on an inclined plane that makes an angle of 26.0o with the horizontal. Make up the plane positive. The coefficient of dynamic friction is .350, and static is .520 A) What are the components of gravity parallel and perpendicular to the plane? What is the force of kinetic friction, and what is the maximum static friction? Would the block be able to remain at rest on the plane? B) Were the block to slide down the plane, what would be its acceleration? (-1.21 m/s/s) C) What force would make the block slide up the plane with an acceleration of 2.40 m/s/s? (+48.9 N) D) What force in what direction would make the block slide down the plane with an acceleration of 0.800 m/s/s? (+2.07 N) E) Suppose there is an outside force of 9.50 N acting up the plane, what other force in what direction would make the block slide down the plane with an acceleration of 1.90 m/s/s down the plane? (-12.9 N)
Whiteboards: Inclined planes 1 | 2 | 3 | 4 | 5 TOC
= 23.5o d = 0.120, s = 0.410 Find F||, and FFd, and FFs max a. Will it stay on the plane if it is at rest? b. If it is sliding freely down the plane, what is its acceleration? 17.603 N 4.858 N 16.598 N W no, and -2.83 m/s/s
= 23.5o d = 0.120, s = 0.410 If it is sliding down the plane, and there is a force of 9.50 N up the plane, what is the acceleration of the block? 17.603 N 4.858 N 16.598 N W -0.721 m/s/s (Down the plane)
= 23.5o d = 0.120, s = 0.410 If it is sliding up the plane, and there is a force of 2.80 N down the plane, what is the acceleration of the block? 17.603 N 4.858 N 16.598 N W -5.61 m/s/s (Down the plane it s decelerating)
= 23.5o d = 0.120, s = 0.410 What force would make it slide up the plane with a deceleration of 1.85 m/s/s? 17.603 N 4.858 N 16.598 N W 14.1 N Up the plane
= 23.5o d = 0.120, s = 0.410 What force would make it accelerate down the plane with an acceleration of 0.750 m/s/s down the plane? 17.603 N 4.858 N 16.598 N W 9.37 N up the plane