Introduction to Counting Techniques in Mathematics
Explore the concept of counting in mathematics using techniques like the Product Rule and Sum Rule. Learn how to calculate the number of possible choices and selections in different scenarios, such as lunch specials, student council selections, exercise schedules, and counting strings. Understand the principles behind these rules and how they can be applied to solve various counting problems efficiently.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Introduction to Counting ICS 6D Sandy Irani
The Product Rule The product rule gives a way to count sequences: Example: lunch special at a restaurant includes a selection of sandwich, side and drink: Sandwiches = {Burger, Grilled chicken, Grilled, cheese} Sides = {Fries, Fruit} Drinks = {Coke, Diet Coke, OJ, Sprite} A lunch selection is specified by a triple: ( [Sandwich], [Side], [Drink] ) For example: (Burger, Fries, Coke) The product rule says that the number of distinct lunch choices is: |Sanwiches| x |Sides| x |Drinks| = 3x2x4 = 24
The Product Rule For finite sets A1, A2, , An : |A1x A2 x x An|=|A1| |A2| |An| Cartesian Product: Elements of this set have the form (a1, a2,.., an) where each aj Aj Can see product rule as a sequence of steps in making a selection: multiply the number of choices at each step The product rule works when the number of choices at each step is independent of the choices made so far.
Product Rule Example An elementary school has 5 4th grade classes. The student council consists of one representative chosen from each class. Let Ci be the set of kids in class i, i = 1, 2, 3, 4, 5 The number of different selection for the student council:
Product Rule Example Athlete training for a triathlon makes her exercise schedule for the week. For each of the 7 days, she can run, swim or bike. How many different schedules are possible?
Counting Strings Set of symbols = How many strings of length n over alphabet ? Product rule says: View as a selection process: how many binary strings of length 4?
The Sum Rule For finite sets A1, A2, , An , If the sets are pairwise disjoint (Ai Aj = , for i j) then |A1 A2 An|=|A1| + |A2| + + |An|
The Sum Rule Lunch Special Selections: Sandwiches = {Burger, Grilled chicken, Grilled, cheese} Sides = {Fries, Fruit} Hot Drinks = {Coffee, Tea, Cocoa} Cold Drinks = {Water, Soda} A lunch selection includes a sandwich, a side and a drink. Sum rule applies because we are picking a hot drink OR a cold drink but not both. Hot Drinks Cold Drinks = |Drinks| = |Hot Drinks Cold Drinks| = |Hot Drinks| + |Cold Drinks| (by Sum Rule) # Selections = |Sandwiches|x|Sides|x|Drinks|
Counting Passwords Digits = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Letters = {A, B, C, D, ., X, Y, Z} How many valid passwords are there if a password must be a string of letters or digits of length 7? be a string of letters or digits of length 7 and start with a letter?
Counting Passwords Digits = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Letters = {A, B, C, D, ., X, Y, Z} How many valid passwords are there is a password must be a string of letters or digits of length 6, 7, or 8?
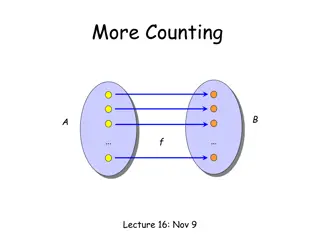
Bijection Rule Let S and T be two finite sets. If there is a bijection from S to T, then |S| = |T| Bijection between a lunch special selection and triples of the form: ( [Sandwich], [Side], [Drink] )
Bijection rule X = {x1, x2, , xn} What is |P(X)|? f: P(X) {0,1}n If f is a bijection, then |P(X)| = |{0, 1}n| = 2n A X, f(A) = y xi A ith bit of y is 1. Example: n = 7, X = {a, b, c, d, e, f, g}
Bijection Rule Example A string is a palindrome if it is the same after it is reversed. Let P6 be the set of all 6-bit strings that are also palindromes. Bijection between {0, 1}3 and P6 f: {0, 1}3 P6 f(x) = xxR (xR is the reverse of x)
K-to-1 Rule Each kid at a slumber party leaves her shoes at the door. To count the number of kids at the party, count the number of shoes and divide by 2.
K-to-1 Rule Let X and Y be finite sets. A k-to-1 correspondence is a function f: X Y such that for each y Y, there are exactly k different x X such that f(x) = y. If there is a k-to-1 correspondence from X to Y then |Y| = |X|/k