Coupling and Mutual Transformation of Acoustic and Gravitational Modes in Kinematically Complex Flows

This study explores the coupling and mutual transformation of acoustic and gravitational modes in kinematically complex flows. The research delves into phenomena such as stratified fluid, internal gravity waves, and formalism related to background flow and compressible cases. The presentation plan covers the explanation of stratified fluid and internal gravity waves, velocity gradient matrix, wave vector components, and equations for derivatives of velocity components. The work sheds light on the interplay of different modes in complex flow scenarios, offering insights into astrophysics and helioseismology.

• Acoustics
• Gravitational Modes
• Kinematic Flows
• Gravity Waves
• Astrophysics

maxx_196 Follow

Uploaded on Sep 11, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. Coupling and mutual transformation of acoustic and gravitational modes in kinematically complex flows. Author: Ia Saralidze Advisor: Andria Rogava Free Univeristy of Tbilisi Reference: Rogava et al. - ACOUSTICS OF KINEMATICALLY COMPLEX SHEAR FLOWS

2. Presentation Plan 01 02 Phenomenon Explanation Stratified fluid and internal gravity waves 03 Main Formalism Description of background flow 04 Compressible Case Future Perspectives After fluctuation fluid is compressible Astrophysics and helioseismology

3. 01 Phenomenon Explanation Stratified fluid and internal gravity waves

4. Phenomenon Explanation Stratified fluid density difference between thin layers. Internal gravity waves is created when we have stratified fluid. Internal waves in uniformly stratified fluid visualized by the displacement of dye lines spaced apart by 5 cm. . o

5. 02 Main Formalism Description of background flow

6. Main Formalism Velocity gradient matrix (shear flow matrix) In the close neighborhood of a point, the spatial variation of the mean velocity can be approximated by a the linear terms in its Taylor expansion. Then a set of nine constants forming the Shear Matrix S: ???,?,? ?0?+ ????? Approximate velocity ??,? ??,? ??,? ??,? ??,? ??,? ??,? ??,? ??,? ?11 ?21 ?31 ?12 ?22 ?32 ?13 ?23 ?33 ? Gradient components

7. Main Formalism Spatially inhomogeneous operator Velocity gradient ? ??+ ??(?,?,?)?? ???+ ????? Fluctuation function Wave number vector ?(?,?,?;?) ?[? ? ,?]??? ? ??? ?? ?0? ??? ?? Main equation for wave vector K ??? + ?? ? = 0 ?? = ????? ?

8. Main Formalism ??,?????????? ?? ? ??? ?????? Equations for derivatives of wave vector components (1)= ??? ?2?? ??,?????????? ?? ? ??? ?????? ?? (1)= ?1??+ ??? ?? ??,?????????? ?? ? ??? ?????? (1)= 0 ?? Equations for derivatives of velocity components (1)+ ???+ ?1??= ??? ?? (1) ???+ ?2??= ??? ?? (1)+ ?1??+ ?2??= ??? ??

9. Main Formalism Equation for derivative of operator D ?(1)= ??? ??+ ??? ??+ ??? ?? Time dependent operator Conserved quantity (1)?? ???? 1= ????? = ??

10. 03 Compressible Case Case where after fluctuation fluid is compressible

11. Compressible Case Main equations for compressible fluid 2D case ?(1)= ????+ ????+ ????+ ???? (1) ???+ ?2??= ??? ?? Pressure perturbation (1)+ ???+ ?1??= ??? ?? (1)= ??? + ??? ?? Density perturbation ?2= ?? Brunt Vaisala s frequency ? = ??2 ?? + ? ?(1)= ?? Derivative of entropy perturbantion

12. Compressible Case Deriving main differential equation 2 1(?? ?? ) 2 1(?? + ?? ) 2+ ?? ???? ???? ????+ ????<=> ??= ?? 2+ ?? ??= ?? (1)= (?1 ?2) Quantities we need to find ?1 ?2 ? ??? = ????? ??(1)= ??? ?2? ?(1)= + ???? ?(1)= ?( , ,?) ?(1)= ??

13. Compressible Case Deriving main differential equation 2+?? (?? 2)(1) 2) 2? +(?? 2 2+?? 2+ ?? (1)= ?? 2) 2+?? (?? ?(1)= ? ??? ? ? ? Main differential equation for coupled system ?(2)+ (?? 2+?2)? = ?? 2? 2+?? (?? 2)1 2) ?(2) (?? 2+2 ?1 ?2 (?? 2)? 2 ????? (?? ?1+ ?? 2+ ?? 2+?? ? = (?? 2+?? 2+?? 2) 2+?? 2)

14. Compressible Case Removing first order derivative from differential equation 2+?? (?? 2)1 2) ? ? ? => 2?(1) => 2?1 = ? =(?? 1=> ? = 1= ln(?? 2+?? 2) 2+ ?? 2 = 2 ln? ?? 2+?? ? ? 2 2+ ?? 2= ? ?2= ?2+ ?1?2 ?? Final differential equations for coupled system ?(2)+ (?? 2+?2)? = ?? 2? ? 3 ? 2? 2 ????? 2 2+ 2?1 ?2 ? ?? ?(2) 2 2+ ? 2 ?? 2 ?????1 ?2 4? ? = ? 3 ?

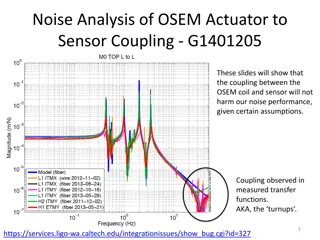
15. Compressible Case Graphical Representation based on referenced paper

16. 04 Future Perspectives Astrophysics and helioseismology

17. Helioseismology

18. Astrophysics

19. Thank You Reference: Rogava et al. - ACOUSTICS OF KINEMATICALLY COMPLEX SHEAR FLOWS Author: Ia Saralidze Advisor: Andria Rogava Free Univeristy of Tbilisi

20. Compressible Case Equation for wave number vector ?2 ?? 2+ ?? 2 (?2)(2)= 4 2?2 2 ?1 ?2 ?(2) ? = 2+ 2 ?4 2?2 ?2 ?1 2 ?(1)= ?2