Understanding Logarithmic Functions and Their Inverses
Mathematically exploring logarithmic functions, their properties, inverse functions, exponential forms, and rewriting logarithmic expressions. Learn how to evaluate logarithms through examples and understand the relationship between exponential and logarithmic forms.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Check up Use your calculator and approximate to three decimal places 32.4 1) 4-1.5 2) e2.3 3)
Check up 2 3) If f(g(x)) = x and g(f(x)) = x, what is know about the functions f(x) and g(x)? 4) If a function passes the horizontal line test, what is know about the function? Find the inverse 5) f(x) = 7x 5
Check up 3 Find the inverse 5) f(x) = 7x 5 6) (-2, 4), (-1, 1), (1, 1), 2, 4)
Chapter 9 Section 3 Logarithmic Functions Page 691.
Do the following Find the inverse of f(x) = bx
Definition Mathematicians have defined a function, called logarithm that allows one to write the inverse of f(x) = bx
Definition of the Logarithmic Function For x > 0 and b > 0, b 1 y = is equivalent to = x logbx by The function f(x) = is the logarithmic function with base b logbx
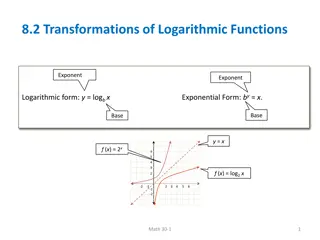
Forms Logarithmic form: y=logbx Exponential form: by=x
Notice Logarithmic form: Where is the exponent and base. y=logbx Exponential form: by=x Base of the logarithm is the base of the exponent.
Rewrite in Exponential Form 3=log5x a) log37=x b) c)
Rewrite in Logarithmic Form 122=x 1) b3=8 2) ey=9 3)
Evaluate Logarithms Rewrite in exponential form, then evaluate Example: Evaluate log216 Solution: 1) Write as an equation: = x 2) Rewrite in exponential form: 3) Solve log216 2x=16
Try log39 a) log366 b) log66 c)
Basic Logarithmic Properties b1=b 1) note: logbb=1 logb1=0 b0=1 2) note: log55 a) log71 b)
Domain of a Logarithmic Function logbg x ( ) Domain of f(x) = consists of all x for which g(x) > 0 ( ) log4x+3 Find the domain of g(x) = Solution: domain consist of all x for which x + 3 > 0. So, solve the inequality, obtain x > - 3 so the domain is ( ) -3,
Common Logarithms Logarithmic function with base 10. Function f(x) = is usually expressed as f(x) = log x. log10x Calculator with LOG key can be used to evaluate common logarithms. Find: a) log 1000 b) log 2.5 Error message or NONREAL ANSWERS, out of the domain
Properties of Common Logarithms General Properties 1) logb1=0 Common Logarithms 1) log 1 = 0 logbb=1 2) 2) log 10 = 1 log10x=x logbbx=x 3) 3) 10log? x=x logbx=x 10 4) 4) 3 and 4 are inverse properties
Natural Logarithms Logarithmic function with base e Function f(x) = usually expressed as f(x) = ln x ln x read el en of x logex Calculator with LN key can be used to evaluate natural logarithms. Domain: f(x) = ln x all values of x > 0
Properties of Natural Logarithms General Properties 1) logb1=0 Natural Logarithms 1) ln 1 = 0 logbb=1 2) 2) ln e = 1 ln? ex=x logbbx=x 3) 3) eln? x=x logbx=x 10 4) 4) 3 and 4 are inverse properties
Try a) log 327 b) log553 c) ln e7
Summary by logbx y = is equivalent to = x Logarithmic and exponential form Evaluation of logarithms Use definition Calculator Common and natural logarithms Logarithm properties.
bx Inverse of f(x) = Step 1: Replace f(x) with y Sep 2: Interchange x and y Step 3: Solve for y Step 4: Replace y with f-1x ( )