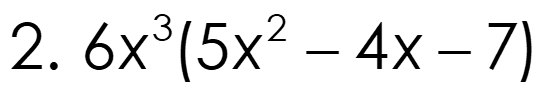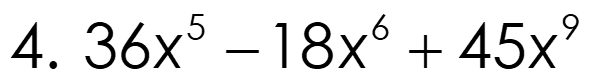Factoring Trinomials and Difference of Two Perfect Squares
Explore the concept of factoring trinomials and difference of two perfect squares through step-by-step examples and visual aids. Understand the sign rules for factoring trinomials with positive and negative last terms. Learn how to factor out a greatest common factor and practice factoring various quadratic expressions effectively.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Opener Multiply 1. (x+3)(2x-7) 3 2 2. 6 (5 x x 4 x 7) Factor 3. 42x 7 5 6 9 4. 36 x 18 x 45 x +
Factoring Trinomials and Difference of Two Perfect Squares
Sign Rule for Factoring Trinomials: When the last term is POSITIVE The signs inside the parenthesis will be the SAME Look at b for the sign Front are factors of a Last factors of c that will add to get b.
x2 +7x + 6 ( )( ) x + 6 x + 1
x2 + 9x + 14 ( )( ) x + 7 x + 2
x2 6x + 8 ( )( ) x 4 x 2
Sometimes you can factor out a GCF 1st!
x2 10x + 16 ( )( ) x 8 x 2
2x2 16x + 24 2(x2 8x +12) 2( )( ) x 6 x 2
Opener.. 3y2 + 36y + 60 3(y +10)(y +2) 4x2 +24x + 32 4(x + 2)(x + 4)
Sign Rule for Factoring Trinomials: When the last term is NEGATIVE The parenthesis will have DIFFERENT SIGNS. The larger factor will have the SAME sign as the middle number
n2 + 2n 48 ( )( ) n + 8 n 6
x2 + 8x 20 ( )( ) x + 10 x 2
x2 4x 21 ( )( ) x + 3 x 7
x2 9x 36 ( )( ) x + 3 x 12
c4 + 2c3 80c2 ( ) 8 + 2 2 2 80 c c c )( ( ) + 2 10 c c c
3x2 + 6x 24 ( ) + 2 3 2 8 x x ( )( ) + 3 4 2 x x
Opener Match the problems with the signs of the factors. A.x2 - 6x + 8 i. Both signs are positive. B.x2 + 6x + 8 ii. Both signs are negative. C. x2 - 7x - 8 iii. They have different signs.
2x3 + 18x2 + 28x ( ) + + 2 2 9 14 x x x ( )( ) + + 2 7 2 x x x
5x2 + 5x 10 ( ) + )( 2 2 5 ( 2 x x ) + 5 1 x x
3x3 6x2 45x ( ( ) 2 3 2 )( 15 ) 3 x x x + 3 5 x x x
3x3 39x2 + 120x ( ( ) ) + 2 3 13 )( 5 40 x x x 3 8 x x x
Difference of Two Perfect Squares
Factoring Difference of Two Squares 1. Both terms must be Perfect Squares and have a MINUS between them 2. Check the binomial for GCF 3. Use two sets of parenthesis (one s a plus, one s a minus) 4. Split up what it takes to make the 1st a perfect square and what it takes the 2nd to be a perfect square
Difference of Two Squares Factor 2 1. 25 n ( n = )( ) + 5 5 n 2 ( 2 2. 4 121 x + x y )( ) = 2 11 2 11 y x y
Difference of Two Squares Factor 2 3. 196r 1 ( 14 = )( ) + 1 14 1 r r x ( 10 2 4. 100 49 + )( ) = 7 10 7 x x
2x3 162x ( ) x x 2 2 81 ( )( ) + 2 9 9 x x x
16x2 36 ( ) x 2 4 4 9 ( )( ) + 4 2 3 2 3 x x
Classwork Worksheet