Journey Through Math Education: From Sea Level to High School
Exploring the progression of mathematical concepts from grade 8 sea level to high school, this journey covers functions, patterns, linear regression, and geometric functions. Students transition through various levels, deepening their understanding and application of mathematical concepts with each step, culminating in the study of inverse functions and formal notations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
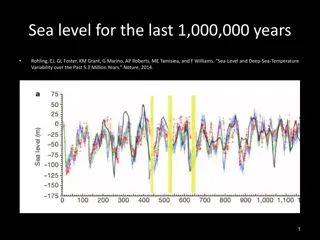
Overall Themes CNN of OJ = CCLS Concepts spiraled and occur in waves. Multiple representations always present Pictures, tables, formulas, graphs Context! Grade 8 = Sea Level
Grade 8 = Sea Level Students first hear the word function in Grade 8. Deep: Input/Output in all representations Shallow: Definition of function A function is a rule that assigns each input to one output. Deep: Linear Functions and y = mx + b Shallow: The existence of nonlinear functions Deep: Using scatterplots to illustrate bivariate data
Back to the Future! Pretend you re back in Kindergarten Eating paste Nap time Skip counting! Patterns!!
Back to the Future! Now, pretend you re back in 3rd Grade Kickball! More Patterns!! Predicting!!!
Back to the Future! Pretend you re back in 4th Grade Pokemon! Patterns!! Measurement!!!
Back to the Future! Pretend you re back in 6th Grade Puberty! Patterns!! Measurement!!! Ratios!!!!
Back to the Future! Pretend you re back in 7th Grade More Puberty! Graphs!! Tables!!! Equations!!!! Direct Variation!!!!!
Back to Sea Level Input/Output in all representations (used for years) First use of the word function LinFun and y = mx + b (proportional reasoning and y = cx) First appearance of nonlinear functions Illustrate bivariate data (began previous year) First appearance of Linear Regression
In High School... Build functions from sequences (discrete to continuous) Model & interpret in context Domain & range Compositions Formal notation: f(x)=... Geometric functions (transformations; specifically translations) Recursive vs. explicit functions (recursive functions emphasize rates of change) Inverse functions
Surprise! Whats new, exciting, strange, or potentially difficult to adapt to? 1.Common theme of informal introduction of ideas, then later formalizing them a. Proportions b. Multiple representations of linear functions c. Nonlinear functions d. Statistics 2. Statistics -- association between two variables, linear/non-linear regression 3. Transformations of functions connected to transformations in geometry 4. NO VERTICAL LINE TEST!