Understanding Open Channel Flow and Mannings Equation

This review covers hydraulic devices such as orifices, weirs, sluice gates, siphons, and outlets for detention structures. It focuses on open channel flow, including uniform flow and varied flow, and explains how to use Mannings equation for calculations related to water depth, flow area, and velocity distribution. The content delves into the characteristics of uniform flow in open channels and provides information on how to solve for flow and velocity using Mannings equation in both English and Metric units.

• Hydraulic devices
• Open channel flow
• Mannings equation
• Water flow
• Flow calculations

zhu_yl Follow

Uploaded on Sep 12, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

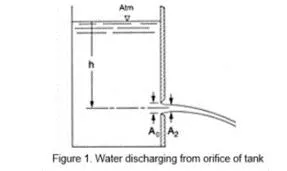
1. CTC 261 Review Hydraulic Devices Orifices Weirs Sluice Gates Siphons Outlets for Detention Structures 1

2. This Week: Open Channel Flow Uniform Flow (Manning s Equation) Varied Flow 2

3. Objectives Students should be able to: Use Manning s equation for uniform flow calculations Calculate Normal Depth by hand Calculate Critical Depth by hand Utilize Flowmaster software for open channel flow problem-solving 3

4. Open Channel Flow Open to the atmosphere Creek/ditch/gutter/pipe flow Uniform flow-EGL/HGL/Channel Slope are parallel velocity/depth constant Varied flow-EGL/HGL/Channel Slope not parallel velocity/depth not constant 4

5. Uniform Flow in Open Channels Water depth, flow area, Q and V distribution at all sections throughout the entire channel reach remains unchanged The EGL, HGL and channel bottom lines are parallel to each other No acceleration or deceleration 5

6. Mannings Equation Irish Engineer On the Flow of Water in Open Channels and Pipes (1891) More: http://www.engineeringtoolbox.com/mannings-roughness-d_799.html https://www.hydrologystudio.com/pulp-friction/ https://www.h2ometrics.com/manning-equation/ 6

7. Mannings Equation-English Solve for Flow Q=AV=(1.486/n)(A)(Rh)2/3S1/2 Where: Q=flow rate (cfs) A=wetted cross-sectional area (ft2) Rh=hydraulic radius=A/WP (ft) WP=wetted perimeter (ft) S=slope (ft/ft) n=friction coefficient (dimensionless) 7

8. Mannings Equation-Metric Solve for Flow Q=AV=(1/n)(A)(Rh)2/3S1/2 Where: Q=flow rate (cms) A=wetted cross-sectional area (m2) Rh=hydraulic radius=A/WP (m) WP=wetted perimeter (m) S=slope (m/m) n=friction coefficient (dimensionless) 8

9. Mannings Equation-English Solve for Velocity V=(1.486/n)(Rh)2/3S1/2 Where: V=velocity (ft/sec) A=wetted cross-sectional area (ft2) Rh=hydraulic radius=A/WP (ft) WP=wetted perimeter (ft) S=slope (ft/ft) n=friction coefficient (dimensionless) 9

10. Mannings Equation-Metric Solve for Velocity V=(1/n)(Rh)2/3S1/2 Where: V=flow rate (meters/sec) A=wetted cross-sectional area (m2) Rh=hydraulic radius=A/WP (m) WP=wetted perimeter (m) S=slope (m/m) n=friction coefficient (dimensionless) 10

11. Mannings Friction Coefficient http://www.lmnoeng.com/manningn.htm Typical values: Concrete pipe: n=.013 CMP pipe: n=.024 11

12. Triangular/Trapezoidal Channels Must use trigonometry to determine area and wetted perimeters 12

13. Pipe Flow Hydraulic radii and wetted perimeters are easy to calculate if the pipe is flowing full or half-full If pipe flow is at some other depth, then tables/figures/software are usually used 13

14. 14

15. Example-Find Q Find the discharge of a rectangular channel 5 wide w/ a 5% grade, flowing 1 deep. The channel has a stone and weed bank (n=.035). A=5 sf; WP=7 ; Rh=0.714 ft S=.05 Q=38 cfs 15

16. Example-Find S A 3-m wide rectangular irrigation channel carries a discharge of 25.3 cms @ a uniform depth of 1.2m. Determine the slope of the channel if Manning s n=.022 A=3.6 sm; WP=5.4m; Rh=0.667m S=.041=4.1% 16

17. Friction loss How would you use Manning s equation to estimate friction loss? 17

18. Using Mannings equation to estimate pipe size Size pipe for Q=39 cfs Assume full flow Assume concrete pipe on a 2% grade Put Rh and A in terms of Dia. Solve for D=2.15 ft = 25.8 Choose a 27 or 30 RCP Also see Appendix A of your book 18

19. Break 19

20. Normal Depth Given Q, the depth at which the water flows uniformly Use Manning s equation Must solve by trial/error (depth is in area term and in hydraulic radius term) 20

21. Normal Depth Example Find normal depth in a 10.0-ft wide concrete rectangular channel having a slope of 0.015 ft/ft and carrying a flow of 400 cfs. Assume n=0.013 (concrete) 21

22. Normal Depth Example Assumed D (ft) 2.00 Area (sqft) 20 Peri. (ft) 14 Rh (ft) 1.43 Rh^.66 Q (cfs) 1.27 356 3.00 30 16 1.88 1.52 640 2.15 21.5 14.3 1.50 1.31 396 22

23. Stream Rating Curve Plot of Q versus depth (or WSE) Also called stage-discharge curve 23

24. Specific Energy Energy above channel bottom Depth of stream Velocity head 24

25. Depth as a function of Specific Energy Rectangular channel Width is 6 Constant flow of 20 cfs 25

26. Specific Energy Start Depth Depth Increment Flow Rect Channel Width g Critical Depth D+v^2/2g 0.2 ft 0.2 ft 20 cfs 6 ft 32.2 ft/sec^2 0.70 ft Depth 0.20 0.40 0.60 0.80 1.00 1.20 1.40 1.60 1.80 2.00 2.20 2.40 2.60 2.80 3.00 Area 1.20 2.40 3.60 4.80 6.00 7.20 8.40 9.60 10.80 12.00 13.20 14.40 15.60 16.80 18.00 Velocity 16.67 8.33 5.56 4.17 3.33 2.78 2.38 2.08 1.85 1.67 1.52 1.39 1.28 1.19 1.11 Specific Energy 4.51 1.48 1.08 1.07 1.17 1.32 1.49 1.67 1.85 2.04 2.24 2.43 2.63 2.82 3.02 26

27. Specific Energy Curve 3.5 3.0 Channel Depth (ft) 2.5 2.0 1.5 1.0 0.5 0.0 0.0 1.0 2.0 3.0 4.0 5.0 Specific Energy (ft) 27

28. Critical Depth Depth at which specific energy is at a minimum Other than critical depth, specific energy can occur at 2 different depths Subcritical (tranquil) flow d > dc Supercritical (rapid) flow d < dc 28

29. Critical Velocity Velocity at critical depth 29

30. Critical Slope Slope that causes normal depth to coincide w/ critical depth 30

31. Calculating Critical Depth a3/T=Q2/g A=cross-sectional area (sq ft or sq m) T=top width of channel (ft/m) Q=flow rate (cfs or cms) g=gravitational constant (32.2/9.81) Rectangular Channel Solve Directly Other Channel Shape-Solve via trial & error 31

32. Critical Depth (Rectangular Channel) Width of channel does not vary with depth; therefore, critical depth (dc) can be solved for directly: dc=(Q2/(g*w2))1/3 For all other channel shapes the top width varies with depth and the critical depth must be solved via trial and error (or via software like flowmaster) 32

33. Froude Number F=Vel/(g*D).5 F=Froude # V=Velocity (fps or m/sec) D=hydraulic depth=a/T (ft or m) g=gravitational constant F=1 (critical flow) F<1 (subcritical; tranquil flow) F>1 (supercritical; rapid flow) 33

34. Varied Flow Rapidly Varied depth and velocity change rapidly over a short distance; can neglect friction hydraulic jump Gradually varied depth and velocity change over a long distance; must account for friction backwater curves 34

35. Hydraulic Jump Occurs when water goes from supercritical to subcritical flow Abrupt rise in the surface water Increase in depth is always from below the critical depth to above the critical depth 35

36. Hydraulic Jump Velocity and depth before jump (v1,y1) Velocity and depth after jump (v2,y2) Although not in your book, there are various equations that relate these variables. Specific energy lost in the jump can also be calculated. 36

37. Hydraulic Jump http://www.ce.utexas.edu/prof/hodges/classes/Hydraulics.html http://krcproject.groups.et.byu.net/ http://www.lmnoeng.com/Channels/HydraulicJump.php Circular hydraulic jumps http://www-math.mit.edu/~bush/jump.htm 37

38. Varied Flow Slope Categories M-mild slope S-steep slope C-critical slope H-horizontal slope A-adverse slope 38

39. Varied Flow Zone Categories Zone 1 Actual depth is greater than normal and critical depth Zone 2 Actual depth is between normal and critical depth Zone 3 Actual depth is less than normal and critical depth 39

40. Water-Surface Profile Classifications H2, H3 (no H1) M1, M2, M3 C1, C3 (no C2) S1, S2, S3 A2, A3 (no A1) 40

41. Water Surface Profiles http://www.fhwa.dot.gov/engineering/hydraulics/pubs/08090/04.cfm 41

42. Water Surface Profiles-Change in Slope http://www.fhwa.dot.gov/engineering/hydraulics/pubs/08090/04.cfm 42

43. Backwater Profiles Usually by computer methods HEC-RAS Direct Step Method Depth/Velocity known at some section (control section) Assume small change in depth Standard Step Method Depth and velocity known at control section Assume a small change in channel length 43