Understanding the Synergy in Computer Systems

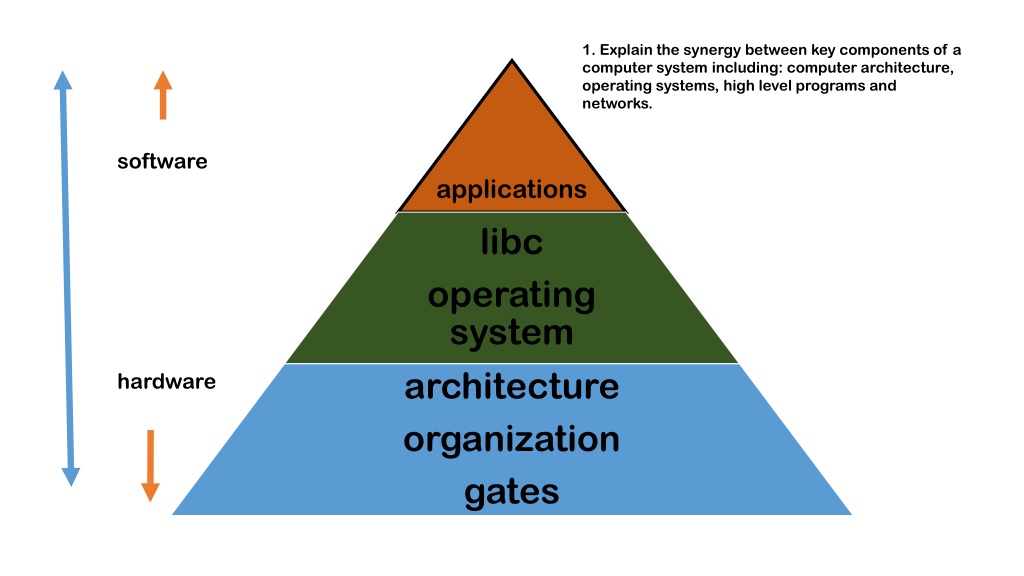
1. Explain the synergy between key components of a computer system including: computer architecture, operating systems, high level programs and networks. software applications libc operating system architecture organization gates hardware

1. components of a computer system including: computer architecture, operating systems, high level programs and networks. Explain the synergy between key Application Algorithms Programming language libC kernel/OS ----------------------------------- ISA Instruction set Architecture Microarchitecture Reg transfer lang ----------------------------- Circuits Gates Physics high level programs operating systems computer architecture computer organization software hardware

logic the basic logic we use Boolean algebra and, or, not which all comes down to nand symbols 0/1, all the stuff they encode namely all the stuff numbers characters/writing systems images, video, audio, everything else (the logic too) models how it all works together to compute open-ended, we ll build a platform for understanding all that is yet to come logic working on symbols to build models

Church Turing Thesis what it means to be a computer Turing machine vs the lambda calculus Alan Turing Alonzo Church (a bit like the clock makers vs the astronomers trying to solve longitude)

Church Turing Thesis Turing machine vs the lambda calculus Alan Turing Alonzo Church https://www.youtube.com/watch?v=dNRDvLACg5Q https://www.youtube.com/watch?v=eis11j_iGMs procedural programming languages C,Java,Pascal functional programming languages lisp, Haskell ( list-based languages)

An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities by George Boole and, or, not these are the same logical operations we use when thinking, and when programming they operate on the symbols (0 and/or 1) our programming languages give us operators to use when writing a program - &&, ||, ^ so we can use this logical reasoning when expressing an algorithm in code to solve a problem

each operation and, or, not has a realization in hardware with a symbol to represent it and gate or gate not gate

computer organization how gates are put together to build the fundamental components of a computer, connect them together, and control operation i.e. to make the computer compute decoders multiplexers counters registers memory

AND gate hungry pizza money if ((hungry==true) && (money==true)) { logic to go get pizza } $ 0 1 0 1 0 0 1 1 0 0 0 1 We call this representation a Truth Table 1 means true 0 means false

OR gate cash my treat credit card if ((cash==true) || (card==true)) { pay the bill } x y (x or y) 0 0 1 1 0 1 0 1 0 1 1 1 Truth Table 1 means true 0 means false

NOT gate Y X x x 0 1 1 0 Truth Table 1 means true 0 means false

how many different possible 2-input gates are there? 16 why?

x y (x or y) 0 0 1 1 0 1 0 1 0 1 1 1 or x y (x and y) 0 0 1 1 0 1 0 1 0 0 0 1 and but also 14 more:

0 0 1 1 0 1 0 1 0 1 0 0 0 0 1 1 0 1 0 1 1 0 0 0 0 0 1 1 0 1 0 1 1 1 0 0 0 0 1 1 0 1 0 1 0 0 0 0 0 0 1 1 0 1 0 1 0 1 0 1 0 0 1 1 0 1 0 1 1 0 0 1 0 0 1 1 0 1 0 1 1 1 0 1 0 0 1 1 0 1 0 1 0 0 0 1 and 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 1 0 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 0 1 0 0 1 0 0 0 1 1 0 1 0 1 0 1 1 1 0 0 1 1 0 1 0 1 1 0 1 1 0 0 1 1 0 1 0 1 1 1 1 1 0 0 1 1 0 1 0 1 0 0 1 1 or

0 0 1 1 0 1 0 1 0 1 0 0 0 0 1 1 0 1 0 1 1 0 0 0 0 0 1 1 0 1 0 1 1 1 0 0 0 0 1 1 0 1 0 1 0 0 0 0 nor false 0 0 1 1 0 1 0 1 0 1 0 1 0 0 1 1 0 1 0 1 1 0 0 1 0 0 1 1 0 1 0 1 1 1 0 1 0 0 1 1 0 1 0 1 0 0 0 1 and 0 0 1 1 0 1 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 1 0 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 0 1 0 0 1 0 xor (exclusive or) nand 0 0 1 1 0 1 0 1 0 1 1 1 0 0 1 1 0 1 0 1 1 0 1 1 0 0 1 1 0 1 0 1 1 1 1 1 0 0 1 1 0 1 0 1 0 0 1 1 or true (tautology)

outputs of the 16 possible gates, written sideways 0000 1000 0001 1001 0010 1010 0011 1011 0100 1100 0101 1101 0110 1110 0111 1111

this is called a NAND gate like an AND gate connected to a NOT gate

and or not nand XY X+Y X X Y X Y X^Y XvY 0 0 0 0 1 1 0 1 0 1 1 1 1 0 0 1 0 1 1 1 1 1 0 0 nand and

What does this do? 0 0 1 1 0 1 0 1 1 1 1 0 nand

What does this do?

What does this do?

What does this do?

What are these? or not and xor

computer organization how gates are put together to build the fundamental components of a computer, connect them together, and control operation i.e. to make the computer compute decoders multiplexers counters registers memory we can build the entire computer with and, or, and not gates, but notice how those are not any of and,or,not ?

We can build each of and, or, not gates by using only nand gates this is called a NAND gate it is an AND gate connected to a NOT gate

usually more than four in a chip, but you can still buy the SN 7400N

nand It s not an easy way to think but it s an easy thing to build and easy to build them super tiny (atomic scale) and they can switch on/off incredible quickly, with fidelity (on the order of 1 trillion times / second 402 terabits/sec as of June 24, 2024 (on commercially available fiber))

so, that is what your computer is made of 109 per second

do all 16 have a name ? here s another: X Y X Y ------------------------- 0 0 0 0 1 1 1 0 1 1 1 0 This one is called exclusive-or (the other or is inclusive-or) The or in use in: Would you like cake or pie for dessert?

exclusive-or is very important, and widely used, in computer graphics, cryptography, among others it is a function with the very useful property that it is its own inverse (more on that later) X Y X Y ------------------------- 0 0 0 0 1 1 1 0 1 1 1 0 (X Y) Y X ---------------------------- 0 0 0 1 1 0 1 0 1 0 1 1 true no matter how many terms, and how much complexity the first term has gives you back X this is how the old rubber rectangle worked smoothly X xor Y xor with y So, are there any others?

Lets leap ahead for a moment to take a shallow look at how we use our symbols to represent numbers (count/quantity) here we are talking only about non-negative integers < 256

0 0 0 1 0 0 1 1 Digit position 7 6 5 4 3 2 1 0 position Taken as a base B number, each place has the value B Base 2 uses 2 symbols Base 10 uses 10 symbols 0 0 10 == 1 10 == 10 10 == 100 10 == 1000 etc 2 == 1 2 == 2 2 == 4 2 == 8 etc 1 1 2 2 3 3 Base K uses K symbols

0 0 0 1 0 0 1 1 128 64 32 16 8 4 2 1 So as a base 2 number, this is 16 + 2 + 1 == 19 another way of thinking about it: represent any non-negative integer as the sum of powers of 2 Byte values range from 0 to 255 (when interpreted as an unsigned number)

This may feel nearly useless, you have to carry every time you try to count past 1? let s count: 0 1 10 11 100 101 110 111 1000 //8 1001 //9 1010 //10 1011 //11 1100 //12 1101 //13 1110 //14 1111 //15, now carry again, but each time I get double //that s it for one symbol, go back to zero and carry: //now we re up to 2 (speaking in base 10, where we re comfortable) //3, but need to carry again now //4 (and already using three positions) //5 //6 //7, need to carry again (but it doesn t feel quite so stupid this time) Physically being able to tell a one from a zero, at tiny scale and immense speed, is not so easy. Check out Wikipedia entry for transistor count. It may seem wasteful, and almost ridiculous, but remember that, in 2022, we stored one symbol in about 10 silicon atoms (whatever atom means, check recent conversation about science and models), and we operate at about 2/3 the speed of light (~ 300 million meters in one second)

It still all comes down to a transistor (William Shockley inter alia) I started the 100 club right there the Holmdel location of the old bell labs with a transistor water tower