Understanding Quantum-Mechanical Model and Electromagnetic Waves

Quantum-Mechanical Model delves into how electrons exist in atoms, shaping the chemical and physical properties of elements. It contrasts metals and non-metals, emphasizes noble gases' inertness, and explains the charges on ions. Additionally, it explores the similarities between electrons and light, highlighting the wave nature of light and electromagnetic radiation. Understanding electromagnetic waves, their amplitude, frequency, and wavelength, sheds light on the behavior of light and its interaction with matter.

• Quantum-Mechanical Model
• Electromagnetic Waves
• Elements Properties
• Light Behavior
• Electron Existence

rma_mc Follow

Uploaded on Sep 22, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. Chapter 7 Quantum-Mechanical Model -explains how e- exist in atoms and how close those e- determine the chemical and physical properties of elements -already studied much of this: -metals vs. non-metals -noble gases inert -charges on ions

2. -electrons and light have much in common Wave Nature of Light electromagnetic radiation (waves)- a type of energy embodied in oscillating electric and magnetic fields -waves move at a constant speed of 3.00X108m/s -this is the speed of light (c) -takes a particle of light 1/7 of a second to circle Earth -this is why you see fireworks before you hear the bang and why you see lightning before you hear thunder -sound travels about 340m/s

3. origin

4. electromagnetic waves amplitude- height of a wave from the origin to the crest or from origin to trough -determines the intensity or brightness of the light, greater amplitude = greater intensity wavelength- ( ) - distance between two adjacent crests (units= m, cm, nm) frequency- ( ) - # of wave cycles that pass through a given point per unit time (units= cycles / sec or 1/s or s-1 or hertz- Hz) -each complete wave cycle begins at the origin and returns to the origin

5. -frequency is directly proportional to the speed at which the wave is traveling- the faster the wave, the higher the frequency -frequency and wavelength are inversely proportional

6. c = c = speed of light (3.00 x 108m/s) = frequency (1/s, s-1, Hz) = wavelength (m, cm, nm(10-9)) = c/ page 285 ex 7.1 for practice 7.1 = c/

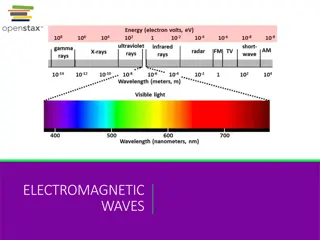
7. visible light- light that can be seen by the human eye -wavelength determines the color of the visible light -can see colors when white light is passed through a prism -red, orange, yellow, green, blue, indigo, violet -red light has the longest wavelength (750nm) -violet has shortest (400nm)

8. electromagnetic spectrum- includes all wavelengths of electromagnetic radiation (radio, microwaves, infrared, visible, UV rays, X-rays, and gamma rays) page 285 figure 7.5 left side = low energy, low frequency, long wavelength right side = high energy, high frequency, short wavelength

9. Types of electromagnetic radiation: radio waves- longest wavelengths, 105, transmits signals for radios, cell phones, TV microwaves- used for radar and microwaves infrared radiation (IR)- the heat you feel when you place your hand near a hot object visible light- light you can see UV rays- from the sun X-rays- used to image bones and internal organs gamma rays ( )- produced by the sun or in space, very dangerous because of high energy

10. interference- waves can cancel each other out or build each other up -depends on alignment upon interaction -if waves of equal amplitude from two sources are in phase, (align with overlapping crests), a wave with twice the amplitude results -this is called constructive interference

12. destructive interference- when waves are completely out of phase and the waves cancel

13. diffraction- when a wave encounters an obstacle or a slit that is comparable in size to its wavelength, it bends around it

14. -diffraction of light through two slits separated by a distance comparable to the wavelength of the light results in an interference pattern -dark lines are waves out of phase -bright lines are waves in phase

15. Particle Nature of Light photoelectric effect- metals emit electrons when light shines on them *especially the alkali metals -used in solar calculators -Einstein proposed that light energy must come in packets photon/quantum- particles/packets of light -he also said that the amount of energy in a photon depends on its frequency

16. E = h E = energy in joules h = Planck s constant = 6.626 x 10 -34J s = frequency (1/s, s-1, Hz) -since = c/ , the energy of a photon can also be expressed as: E = hc -to find number of photons = Epulse / Ephoton

17. -electrons emit light when they are excited by the passage of an electric discharge through an element atomic emission spectrum- range of wavelengths emitted by a particular element that can be used to identify an element ex- neon lights- each noble gas will give a specific color (He= pink, Ne= orange/red, Xe= blue, Kr= whitish) ex- fireworks- each element present will give a particular color (Na= yellow, Sr= red, Ca= orange) page 292

19. -Neils Bohr said that e- travel around the nucleus in circular orbits (energy levels) *e- are at fixed distances from nucleus *radiation was emitted or absorbed only when an electron jumped from one level to another

20. Louis de Broglie -stated that a single electron traveling through space has a wave nature -its wavelength is related to its kinetic energy = h/mv v = h/m = wavelength h = Planck s constant (6.626x10-34J s) m = mass of electron (9.11x10-31kg) v = velocity (m/s) **1J = 1kg m2/s2

21. Example- Calculate the wavelength of an electron traveling with a speed of 2.65x106m/s = h/mv (6.626x10-34 kgm2/s2 s) (9.11x10-31kg)(2.65x106m/s) =2.74 x 10-10m For Practice 7.4 page 297

22. Heisenbergs Uncertainty Principle -states that it is impossible to know both the velocity and position of a particle at the same time -Remember where electrons are found in an atom!! -surrounding the nucleus in electron clouds or energy levels

23. Quantum Mechanics and the Atom Principal Quantum Number (n) -the energy level -determines the overall size and energy of an orbital (where electrons are held) -n can be equal to 1, 2, 3, 4, 5, 6, 7 -distance electron is from the nucleus increases as n increases

24. Angular Momentum Quantum Number (l) -determines the shape of the orbital -shapes are s, p, d, or f -when given a value of n, l can be any integer including zero up to n - 1 ex: n = 1 l = 0 ex: n = 2 l = 0, 1 -to avoid confusion between n and l, values of l are often assigned as letters

25. Value of l l = 0 l = 1 l = 2 l = 3 Back to examples: #1: n = 1 l = 0 is in first energy level with s orbitals #2: n = 2 l = 0, 1 is in the second energy level with s and p orbitals Shape of orbital s p d f

26. Atomic Orbital Shapes s-orbital -spherically shaped -one shape, one orbital -lowest energy orbital p-orbital -peanut/dumb bell shaped -three shapes, three orbitals d-orbital -clover shaped -five shapes, five orbitals

27. f-orbitals -flower shaped -7 shapes, 7 orbitals energy level n = 1 n = 2 n = 3 n = 4 # of sublevels Type of sublevel 1 2 3 4 3s, 3p, 3d 4s, 4p, 4d, 4f 1s 2s,2p

28. ex: how many orbitals in 3d? how many orbitals in 4s? how many orbitals in 2p? how many orbitals in 2s? how many orbitals in the third energy level? 9 1 from s, 3 from p, 5 from d 5 1 3 1

29. -Orbitals with the same value of n are said to be in the same principal level -Orbitals with the same value of n and l are said to be in the same sublevel Magnetic Quantum Number (ml) -specifies the orientation of the orbital -equal to integer values, including zero ranging from -l to +l ex: l = 0 ml = 0 ex: l = 1 ml = -1 0 +1

30. ex: What are the quantum numbers and names of the orbitals in the n = 4 principal level? How many orbitals exist? n = 4 l ml values 0 0 1 -1 0 +1 2 -2 -1 0 +1 +2 4d 3 -3 -2 -1 0 +1 +2 +3 4f **16 total orbitals Try For Practice 7.5 page 303 Example 7.6 page 303 For Practice 7.6 page 303 orbitals 4s 4p

31. electron configuration- how e- are arranged around the nucleus Rules for e- configs: 1) Aufbau Principle -electrons enter orbitals of lower energy first s p d f -atomic orbitals are represented as boxes s = 1 box (1 orbital) p = 3 boxes (3 orbitals) d = 5 boxes (5 orbitals) f = 7 boxes (7 orbitals)

32. 2) Pauli-Exclusion Principle -an atomic orbital can hold at most 2 e- -electrons are represented as arrows -spins are opposite -first electron is -second electron is -number of e- must equal number of arrows

33. 3) Hunds Rule -one electron enters each orbital of equal energy until orbitals contain one electron, then they can hold two e- -it is more stable to have partially filled orbitals than empty orbitals