Understanding Integer Representation in Computer Memory
Explore the binary representation of integers in computer memory, covering decimal, nonal, octal, trinary, and binary numbering systems. Learn how integers are stored using sequences of bits and decipher the breakdown of numbers in different bases. Discover the Arabic digits in decimal representation and delve into the unique characteristics of nonal numbering. Gain insights into the jargon of number breakdowns and their pronunciation.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
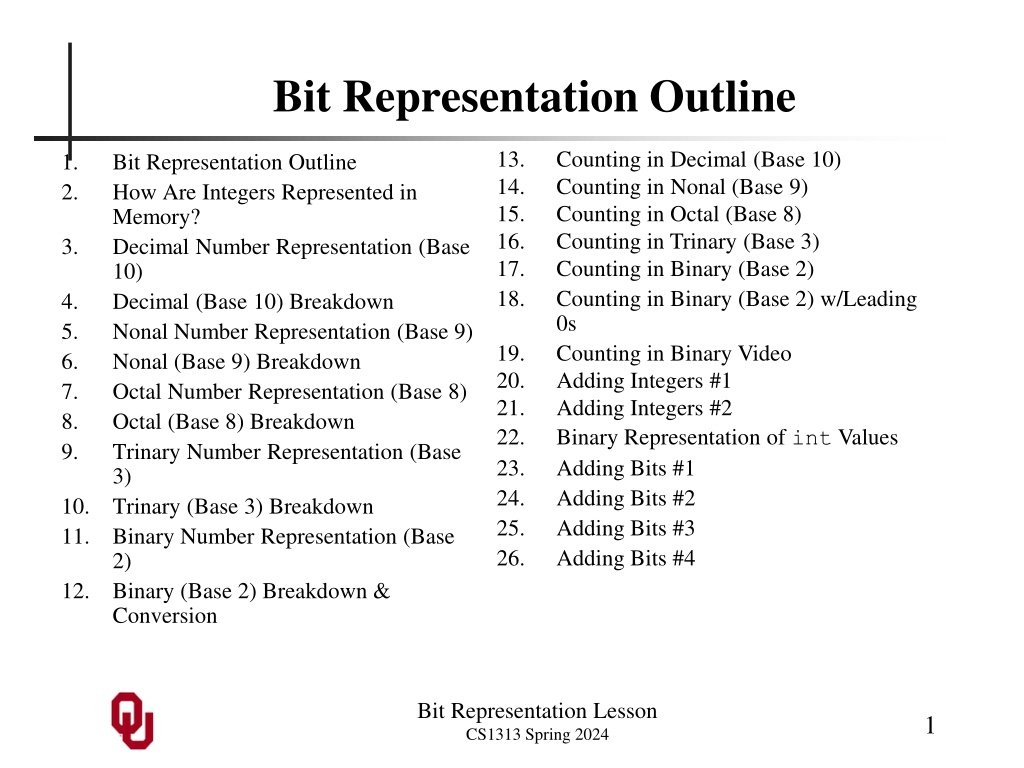
Bit Representation Outline 13. 14. 15. 16. 17. 18. Counting in Decimal (Base 10) Counting in Nonal (Base 9) Counting in Octal (Base 8) Counting in Trinary (Base 3) Counting in Binary (Base 2) Counting in Binary (Base 2) w/Leading 0s Counting in Binary Video Adding Integers #1 Adding Integers #2 Binary Representation of int Values Adding Bits #1 Adding Bits #2 Adding Bits #3 Adding Bits #4 1. 2. Bit Representation Outline How Are Integers Represented in Memory? Decimal Number Representation (Base 10) Decimal (Base 10) Breakdown Nonal Number Representation (Base 9) Nonal (Base 9) Breakdown Octal Number Representation (Base 8) Octal (Base 8) Breakdown Trinary Number Representation (Base 3) Trinary (Base 3) Breakdown Binary Number Representation (Base 2) Binary (Base 2) Breakdown & Conversion 3. 4. 5. 6. 7. 8. 9. 19. 20. 21. 22. 23. 24. 25. 26. 10. 11. 12. Bit Representation Lesson CS1313 Spring 2024 1
How Are Integers Represented in Memory? In computers, alldata are represented as contiguous sequences of bits. An integer is represented as a sequence of 8, 16, 32 or 64 bits. For example: 97 = 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 What does this mean??? Bit Representation Lesson CS1313 Spring 2024 2
Decimal Number Representation (Base 10) In the decimalnumber system (base 10), we have 10 digits: 0 1 2 3 4 5 6 7 8 9 We refer to these as the Arabicdigits. For details, see: http://en.wikipedia.org/wiki/Arabic_numerals Bit Representation Lesson CS1313 Spring 2024 3
Decimal (Base 10) Breakdown = 472110 400010 70010 2010 103102101100 4 7 + 2 1 + + = 110 4. 7. 2. 1. 4. 7. 2. 1. 100010 10010 1010 + Jargon: 472110 is pronounced four seven two one base 10, or four seven two one decimal. + + = 110 103 + 102 + 101 + 100 Bit Representation Lesson CS1313 Spring 2024 4
Nonal Number Representation (Base 9) In the nonalnumber system (base 9), we have 9 digits: 0 1 2 3 4 5 6 7 8 NOTE: No one uses nonal in real life; this is just an example. Bit Representation Lesson CS1313 Spring 2024 5
Nonal (Base 9) Breakdown 47219 = 40009 + 7009 + 209 + . . . . 4 72910 + 8110 + 910 + 110 7 2 1 = 350210 19 = 4. 7. 2. 1. 4. 7. 2. 1. 10009 + 1009 + 109 + 19 = 93+ So: 47219=350210 93 4 92 7 91 2 90 1 92+ Jargon: 47219 is pronounced four seven two one base 9, or four seven two one nonal. 91+ 90= Bit Representation Lesson CS1313 Spring 2024 6
Octal Number Representation (Base 8) In the octal number system (base 8), we have 8 digits: 0 1 2 3 4 5 6 7 NOTE: Some computer scientists used to use octal in real life, but it has mostly fallen out of favor, because it s been supplanted by base 16 (hexadecimal). Octal does show up a little bit in C character strings. Bit Representation Lesson CS1313 Spring 2024 7
Octal (Base 8) Breakdown 47218 = 40008 + 7008 + 208 + . . . . 4 51210 + 6410 + 810 + 110 7 2 1 = 251310 18 = 4. 7. 2. 1. 4. 7. 2. 1. 10008 + 1008 + 108 + 18 = 83+ So: 47218=251310 83 4 82 7 81 2 80 1 82+ Jargon: 47218 is pronounced four seven two one base 8, or four seven two one octal. 81+ 80= Bit Representation Lesson CS1313 Spring 2024 8
Trinary Number Representation (Base 3) In the trinary number system (base 3), we have 3 digits: 0 1 2 NOTE: No one uses trinary in real life; this is just an example. Bit Representation Lesson CS1313 Spring 2024 9
Trinary (Base 3) Breakdown 20213 = 20003 + 03 + 203 + . . . . 2 2710 + 910 + 310 + 110 0 2 1 = 6110 13 = 2. 0. 2. 1. 2. 0. 2. 1. 10003 + 1003 + 103 + 13 = 33+ So: 20213=6110 33 2 32 0 31 2 30 1 32+ Jargon: 20213 is pronounced two zero two one base 3, or two zero two one trinary. 31+ 30= Bit Representation Lesson CS1313 Spring 2024 10
Binary Number Representation (Base 2) In the binary number system (base 2), we have 2 digits: 0 1 This is the number system that computers use internally. Bit Representation Lesson CS1313 Spring 2024 11
Binary (Base 2) Breakdown & Conversion 011000012 = . . . 0 100000002+ 0 27+ 0 12810+ . . . 1 10000002+ 1 26+ 1 6410+ . . . 1 1000002+ 1 25+ 1 3210+ . . . 0 100002+ 0 24+ 0 1610+ . . . 0 10002+ 0 23+ 0 810+ . . . 0 1002+ 0 22+ 0 410+ . . . 0 102+ 12= 0 21+ 0 210+ 110= 9710 . . . 20= 1 1 1 27 0 26 1 25 1 24 0 23 0 22 0 21 0 20 1 9710 = Bit Representation Lesson CS1313 Spring 2024 12
Counting in Decimal (Base 10) In base 10, we count like so: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, ... 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, ... 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, ... 991, 992, 993, 994, 995, 996, 997, 998, 999, 1000, ... Bit Representation Lesson CS1313 Spring 2024 13
Counting in Nonal (Base 9) In base 9, we count like so: 0, 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20, 21, 22, 23, 24, 25, 26, 27, 28, 30, ... 81, 82, 83, 84, 85, 86, 87, 88, 100, 101, 102, 103, 104, 105, 106, 107, 108, 110, ... 181, 182, 183, 184, 185, 186, 187, 188, 200, ... 881, 882, 883, 884, 885, 886, 887, 888, 1000, ... Bit Representation Lesson CS1313 Spring 2024 14
Counting in Octal (Base 8) In base 8, we count like so: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, 22, 23, 24, 25, 26, 27, 30, ... 71, 72, 73, 74, 75, 76, 77, 100, 101, 102, 103, 104, 105, 106, 107, 110, ... 171, 172, 173, 174, 175, 176, 177, 200, ... 771, 772, 773, 774, 775, 776, 777, 1000, ... Bit Representation Lesson CS1313 Spring 2024 15
Counting in Trinary (Base 3) In base 3, we count like so: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212, 220, 221, 222, 1000, ... Bit Representation Lesson CS1313 Spring 2024 16
Counting in Binary (Base 2) In base 2, we count like so: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 10000, ... Bit Representation Lesson CS1313 Spring 2024 17
Counting in Binary (Base 2) w/Leading 0s In base 2, we sometimes like to put in leading zeros, so that the number of bits is a constant (for example, 8 bits, meaning one byte): 00000000, 00000001, 00000010, 00000011, 00000100, 00000101, 00000110, 00000111, 00001000, 00001001, 00001010, 00001011, 00001100, 00001101, 00001110, 00001111 00010000, ... Bit Representation Lesson CS1313 Spring 2024 18
Counting in Binary Video https://img-9gag-fun.9cache.com/photo/aq7Q4AZ_460svvp9.webm Bit Representation Lesson CS1313 Spring 2024 19
Adding Integers #1 128 64 32 16 8 4 2 1 27 0 26 1 25 1 24 0 23 0 22 0 21 0 20 1 9710 = + 1510 = 0 0 0 0 1 1 1 1 11210 = 0 1 1 1 0 0 0 0 Bit Representation Lesson CS1313 Spring 2024 20
Adding Integers #2 128 64 32 16 8 4 2 1 27 0 26 1 25 1 24 0 23 0 22 0 21 0 20 1 9710 = + 0610 = 0 0 0 0 0 1 1 0 10310 = 0 1 1 0 0 1 1 1 Bit Representation Lesson CS1313 Spring 2024 21
Binary Representation of int Values % cat xadd.c #include <stdio.h> int main () { /* main */ int x; x : ? ? ? ? ? ? ? ? x = 97; printf("%d\n", x); x = x + 6; printf("%d\n", x); return 0; } /* main */ % gcc -o xadd xadd.c % xadd 97 103 0 1 1 0 0 0 0 1 0 1 1 0 0 1 1 1 Bit Representation Lesson CS1313 Spring 2024 22
Adding Bits #1 How does a binary bitwise adder actually work? The following is an example solution, but not how it s actually done. Consider adding a bit to a bit. You ll get a sum bit and a carry bit. 0 + 0 = 0 carry the 0 0 + 1 = 1 carry the 0 1 + 0 = 1 carry the 0 1 + 1 = 0 carry the 1 sum = addend XOR augend = (addend OR augend) AND (NOT(addend AND augend)) carry = addend AND augend Bit Representation Lesson CS1313 Spring 2024 23
Adding Bits #2 After you add a bit to a bit, you get the sum bit and the carry bit. That s what will happen for the rightmost bit of a byte or a word. But what about the next-to-rightmost bit? The next-to-rightmost bit (and all other bits to the left of the rightmost bit) will be the sum of the previous (to the right) carry bit plus the addend bit plus the augend bit in that bit s place: previous_carry + addend + augend: 0 + 0 + 0 = 0 carry 0 1 + 0 + 0 = 1 carry 0 0 + 0 + 1 = 1 carry 0 1 + 0 + 1 = 0 carry 1 0 + 1 + 0 = 1 carry 0 1 + 1 + 0 = 0 carry 1 0 + 1 + 1 = 0 carry 1 1 + 1 + 1 = 1 carry 1 Bit Representation Lesson CS1313 Spring 2024 24
Adding Bits #3 previous_carry + addend + augend: 0 + 0 + 0 = 0 carry 0 0 + 0 + 1 = 1 carry 0 0 + 1 + 0 = 1 carry 0 0 + 1 + 1 = 0 carry 1 sum = ((NOT previous_carry) AND (NOT addend) AND augend) OR ((NOT previous_carry) AND addend AND (NOT augend)) OR (previous_carry AND (NOT addend) AND (NOT augend)) OR (previous_carry AND addend AND augend) new_carry = (previous_carry AND addend) OR (previous_carry AND augend) OR (addend AND augend) Bit Representation Lesson CS1313 Spring 2024 1 + 0 + 0 = 1 carry 0 1 + 0 + 1 = 0 carry 1 1 + 1 + 0 = 0 carry 1 1 + 1 + 1 = 1 carry 1 25
Adding Bits #4 You can add a pair of binary numbers of whatever number of bits (for example, 8 bits, 16 bits, 32 bits, 64 bits) by having a series of bitwise adders, each of which takes as its input the associated bits from the addend and augend, plus the carry bit from the previous bit to its right. (The exception is that the rightmost bit s carry bit is always zero.) So a binary adder is very cheap to build! Bit Representation Lesson CS1313 Spring 2024 26