Understanding Equivalence Class Testing and Its Application in Software Testing

Equivalence class testing is a software testing technique that involves dividing input values into classes for effective testing coverage. Equivalence classes are defined mathematically as subsets of a given set, ensuring partitioning and mutual exclusivity. By applying equivalence partitioning, testers select representative values from each class. This method, combined with boundary value analysis, helps streamline testing efforts. The concept is illustrated through examples and test cases, demonstrating the practical application of equivalence class testing in software development.

• Equivalence Class Testing
• Software Testing
• Equivalence Partitioning
• Boundary Value Analysis
• Testing Techniques

apple Follow

Uploaded on Aug 01, 2024 | 1 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. Equivalence Class Testing

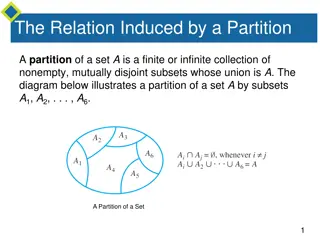
2. Mathematical definition of Equivalence Classes Given a set S, the equivalence classes of S are the subsets S1, S2, , Sn such that S1 S2 Sn = S Si Sj = {}, for 1 <= i, j <= n, i j The first condition asserts that the subsets are partitions of the given set S The second condition asserts that the subsets are mutually exclusive All members of a given subset Si have equal privileges. 2

3. An Example Given A = {1,2,3, ,20} The subsets are {1,13,17,5,9}, {18,6,2,14,10}, {19,11,7,15,3} and {16,8,20,4,12} How do we ensure that the above partitions are equivalence classes? Apply the mathematical definition and check 3

4. Equivalence Partitioning applied to Testing It is almost impossible to test all possible values of a function By applying Equivalence Partitioning method, a tester divides the domain of values into equivalence classes chooses one or few values from each domain The understanding is that each value in an equivalent class serves as a representative for the entire equivalence class Theoretically justified based on the concept of equivalence relation 4

5. Example function with one parameter Consider the function factorial (int x) The equivalence partitions are S1 = {all negative integers} S2 = {0,1} S3 = {all positive integers > 1} Check whether the partitions are indeed equivalence classes 5

6. Test cases from Equivalence Class Testing Serial No. Partition Input Expected output 1 S1 -2 Error 2 S2 0 1 3 S3 3 6 6

7. Combining Equivalence class testing with Boundary Value Analysis Define equivalence classes first Apply boundary value analysis for each equivalence class 7

8. Example Give equivalence partitions and test data for the following function A telephone company uses the following rate structure for long- distance calls Call duration <= 20 min $0.05 per minute Call duration > 20 min $1.00 + $0.10 for every additional minute over 20 min. Maximum duration of a call is 3 hours. Customer is charged only for 3 hours even if the duration exceeds 3 hours. Call duration is always rounded to the nearest minute. 8

9. Equivalence partitions There is only one input - call duration t. There are 3 partitions S1 = {0 <= t <= 20} S2 = {21 <= t <= 180} S3 = {t >= 181} Notice that we do not create partitions for the rate even though it may be considered as an input for this problem. 9

10. Test cases Call duration t Charge ($) Call duration t Charge($) -1 Error 22 1.20 0 0.00 102 9.20 1 0.05 179 16.90 10 0.50 180 17.00 19 0.95 181 17.00 20 1.00 182 17.00 21 1.10 195 17.00 10

11. Another example A bank gives interest for the balance in accounts according to the following: For the first $3000, If it is a checking account, the interest rate is 0% If it is a savings account, the interest rate is 1.5% For balance between $3001 to $10000, both inclusive, If it is a checking account, the interest rate is 2% If it is a savings account, the interest rate is 4% For balance above $10000, If it is a checking account, the interest rate is 4% If it is a savings account, the interest rate is 6% 11

12. Equivalence partitions There are two inputs balance and type of account For balance, there are three partitions: S1 = {0 <= b <= 3000} S2 = {3001 <= b <= 10000} S3 = {b >= 10001} For type of account, there are two partitions T1 = {checking account} T2 = {savings account} 12

13. Interest calculation For this problem, we consider the duration of the balance in years as another input. Assume that the interest is calculated for a maximum of 10 years. We use boundary value analysis for this input, and hence consider the following values: {-1, 0, 1, 4, 9, 10, 11} 13

14. Some Some test cases Balance($) Type of account Duration (years) Interest($) -1 Checking 4 Error 0 Checking 4 0 1 Checking 4 0 1500 Checking 4 0 2999 Checking 4 0 3000 Checking 4 0 3001 Checking 4 240.08 3002 Checking 4 240.16 5000 Checking 4 400.00 9999 Checking 4 792.00 10000 Checking 4 800.00 10001 Checking 4 1600.16 12000 Checking 4 1920.00 14

15. Some Some more test cases Balance($) Type of account Duration (years) Interest($) -1 Savings 9 Error 0 Savings 9 0 1 Savings 9 0.14 1500 Savings 9 202.50 2999 Savings 9 404.87 3000 Savings 9 405.00 3001 Savings 9 1080.36 3002 Savings 9 1080.72 5000 Savings 9 1800.00 9999 Savings 9 3599.64 10000 Savings 9 3600.00 10001 Savings 9 3600.36 12000 Savings 9 4320.00 15

16. Equivalence Class Testing for 2-variable function Consider a function f(x1,x2) where the values of x1 and x2 are defined to be a<= x1 <= b and c<= x2 <=d Assume the following equivalence classes for x1 {a,a+1, ,ta},{ta+1,ta+2, ,tb},{tb+1,tb+2, ,b} Assume the following equivalence classes for x2 {c,c+1, ,tc},{tc+1,tc+2, ,td}, {td+1,td+2, ,d} 16

17. x2 d td tc c a ta tb b x1 Graphical Representation of Equivalence classes for a 2-variable function f(x1,x2) 17

18. Equivalence Class Testing x2 d td tc c a ta tb b x1 18

19. Completeness The Cartesian product guarantees that we have a notion of Completeness We cover all the equivalence classes We have one of each possible combinations of inputs 19

20. X2 d td tc c a ta tb b X1 Equivalence classes with Boundary Value Analysis 20

21. Limitation Equivalence partitioning method assumes that every element in the same equivalence class has same characteristics as every other element in that equivalence class. In some applications, it may be hard to generate such equivalence classes.