The Interaction of Light and Matter
The interaction of light and matter is a fundamental aspect that adds allure to life. Understanding why light is absorbed or transmitted by specific mediums lies in its ability to induce vibrational motion in charged particles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
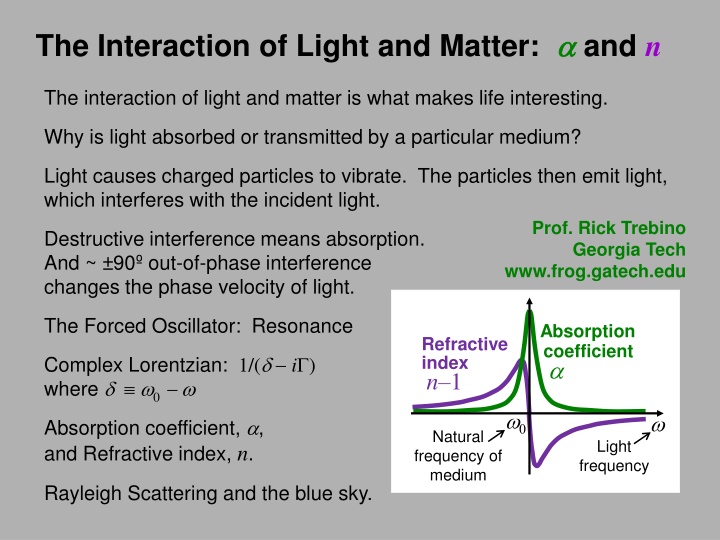
The Interaction of Light and Matter: and n The interaction of light and matter is what makes life interesting. Why is light absorbed or transmitted by a particular medium? Light causes charged particles to vibrate. The particles then emit light, which interferes with the incident light. Prof. Rick Trebino Georgia Tech www.frog.gatech.edu Destructive interference means absorption. And ~ 90 out-of-phase interference changes the phase velocity of light. The Forced Oscillator: Resonance Absorption coefficient Refractive index n 1 Complex Lorentzian: 1/( i ) where 0 Absorption coefficient, , and Refractive index, n. Natural frequency of medium Light frequency Rayleigh Scattering and the blue sky.
Forward vs. Rayleigh Scattering Forward scattering from molecules yields the absorption coefficient and refractive index. Rayleigh scattering (in all other directions) from molecules yields the blue sky. Rayleigh- scattered beams Forward scattering is important mainly near resonance ( = 0). Transmitted beam Input beam 0 Forward- Rayleigh scattering occurs far from resonance ( << 0). scattered beam Rayleigh- scattered beams
Adding Complex Amplitudes When two waves add together with the same complex exponentials, we add the complex amplitudes, E0 + E0'. Constructive interference: Destructive interference: Quadrature phase, 90 , interference: 1.0 1.0 1.0 + + + 0.2 -0.2 -0.2i = = = 1.2 0.8 1-0.2i time time time Slower phase velocity (when accumulated over distance) Laser Absorption
Light excites atoms, which then emit light that interferes with the input light. When light of frequency excites an atom with resonant frequency 0: Electric field at atom Emitted field Electron Incident light + ( ) t ( ) t ( ) ex t E E Emitted light = Transmitted light On resonance ( = 0) An excited atom vibrates at the frequency of the light that excited it and emits energy as light of that frequency. The crucial issue is the relative phase of the incident light and this emitted light. For example, if these two waves are ~180 out of phase, the beam will be attenuated. We call this absorption.
What do you think is happening here? Resonance!
The Forced Oscillator and Resonance When we apply a periodic force to a natural oscillator (such as a pendulum, spring, swing, or atom), the result is a forced oscillator. Examples: Child on a swing being pushed Periodically pushed pendulum Bridge in wind or an earthquake Electron in a light wave Tacoma Narrows Bridge oscil- lating and collapsing because oscillatory winds blew at its resonance frequency. Nucleus in a light wave The forced oscillator is one of the most important problems in physics. It is the concept of resonance.
Electric field at nucleus The Forced Oscillator: The amplitude and relative phase of the oscillator motion with respect to the input force depend on the frequencies. Nucleus Below resonance << 0 Weak vibration. In phase. Strong vibration. 90 out of phase. On resonance = 0 Let the oscillator s reso- nant frequency be 0, and the forcing frequency be . Let the forcing function be a light electric field and the oscillator a (positively charged) nucleus in a molecule. Weak vibration. 180 out of phase. Above resonance >> 0
Electric field at electron The amplitude and relative phase of an electron s motion with respect to incident light also depend on the frequencies. Electron Below resonance << 0 Weak vibration. 180 out of phase. On Strong vibration. -90 out of phase. resonance = 0 The electron charge is negative, so there s a 180 phase shift in all cases (compared to the previous slide s plots). Above resonance >> 0 Weak vibration. In phase.
The amplitude and relative phase of emitted light with respect to the incident light depend on the frequencies. Electric field at atom Emitted field Electron Below resonance << 0 Weak emission. 90 out of phase. Strong emission. 180 out of phase. On resonance = 0 Maxwell s Equations will yield emitted light that s -90 phase- shifted with respect to the atom s motion. Weak emission. -90 out of phase. Above resonance >> 0
The Simple Harmonic Oscillator Consider an electron with position Re{xe(t)}. If it s attracted to a nucleus (assuming it s like a spring), there will be a restoring force. Using Newton s Second Law (F = mea, where me is the electron mass): Restoring force, F m a = 2 2 2 0 / m d x dt m x ( ) ex t e e e e 0 = ( ) exp( ) x t x i t The solution is: 0 0 e e So the electron oscillates at its natural frequency ( 0). The complex amplitude xe0 will depend on other factors. This is a model of any type of oscillator.
Simple Harmonic Oscillator = ( ) exp( ) x t x i t 0 0 e e ( ) ex t The motion is sinusoidal. Simple harmonic motion time But many forces act to slow down motion. For example, atoms spontaneously decay to the ground state after a random time (and so stop oscillating). So the average motion of many electrons is a decaying exponential. ( ) ex t exp( t) The probability of decay is exp( t). Damped simple harmonic motion time
Dephasing and the Damping Factor Also, the vibration of a medium is the sum of the vibrations of all the atoms in the medium, and collisions cause cancellations in the sum. Collisions (1)( ) ex t Collisions dephase the vibrations, reducing the total medium vibration, also exponentially. Atom #1 (2)( ) ex t Atom #2 (3)( ) ex t Atom #3 exp( t) Sum is often called the dephasing rate. time
The Damped Oscillator The equation of motion must include a damping-force term, proportional to the velocity: Restoring force, F Damping force, Fd where we ll assume that the damping is very weak: 0. m a + + = 2 2 2 0 / 2 / 0 m d x dt m d x dt m x e e e e e e ( ) exp( )exp( 2 ) x t x i t t The solution is: 0 0 e e This solution is only approximate, especially in the limit of very strong damping. But, in optics, the damping is usually very weak, so it will suffice for our purposes. ( ) ex t exp( t) Damped simple harmonic motion time
The Forced Oscillator Consider an electron on a spring with positionxe(t), now driven by a light wave, E(t) =E0 exp( i t). The equation of motion becomes: Lorentz force from the light wave Damping force Restoring force m a + + = e is the electron charge i t 2 2 2 0 / 2 / exp( ) m d x dt m dx dt m x eE 0 e e e e e e The solution is: ( ) E t ( ) t ( ) ex t E / e m = i t ( ) exp( ) e x t E 0 e 2 0 2 2 i Now the electron oscillates at the incident light-wave frequency , not the electron s natural frequency 0. It has a complex amplitude that depends on , 0, and .
Checking Our Solution ( ) E t + + = i t 2 2 2 0 / 2 / exp( ) m d x dt m dx dt m x eE 0 e e e e e e / e m Substitute the solution for xe(t) to see if it works: = ( ) ( ) e x t E t e 2 0 2 2 i Immediately cancel the factor of E(t) in all terms. = i t ( ) exp( ) E t E where 0 / / e m e m ( ) ( ) 2 + + 2 e e m i m i e e 2 0 2 2 0 2 2 2 i i = / e m 2 0 e m e Multiply both sides by : 0 e 2 0 2 2 i 2 2 2i ( ) ( ) ( ) ( )( ) ( ) 2 + + = 2 0 2 0 2 / 2 / / 2 m i e m m i e m m e m e i e e e e e e
Checking Our Solution (contd) ( ) ( ) ( ) ( )( ) ( ) 2 + + = 2 0 2 0 2 / 2 / / 2 m i e m m i e m m e m e i e e e e e e Canceling the electron masses: ( ) ( ) ( ) + + = 2 2 0 2 0 2 2 2 e e i e e i Multiplying everything out and canceling common terms: + = 2 2 0 2 0 2 2 2 e ie e e e ie QED So the solution for the electron motion is: Notice that, if damping weren t present, the amplitude would go to when = . / e m = ( ) ( ) e x t E t e 2 0 2 2 i
Damped-Forced-Oscillator Solution for Light-Driven Atoms The forced-oscillator response is sinusoidal, with a relative phase that depends on the frequencies involved: Here, e< 0. Also, , >> / 1 e m = ( ) ( ) ( ) e x t E t E t e 2 0 2 2 0 2 2 2 i i The electron vibrates 180 out of phase with the light wave. Vibration magnitude is small. 1 When << 0: ( ) ( ) ( ) ex t E t E t 2 0 The electron vibrates -90 out of phase with the light wave. Vibration magnitude is large. 1 i When = 0: ( ) ( ) ( ) ex t E t iE t 2 The electron vibrates in phase with the light wave. Vibration magnitude is small. 1 When >> 0: ( ) ( ) ( ) ex t E t E t 2
Electric field at atom The amplitude and relative phase of an electron s motion with respect to incident light depend on the frequencies. Electron Weak vibration. 180 out of phase. Below resonance << 0 On Strong vibration. -90 out of phase. resonance = 0 Recall that the atom s resonant frequency is 0, and the light frequency is . Above resonance >> 0 Weak vibration. In phase.
The atoms response is approximately a Complex Lorentzian. / / e m e m = ( ) e e x t Consider: e + ) 2 2 0 2 2 ( )( i i 0 0 / e m Assuming 0, 0 + 2 , so this becomes: = e 2 ( / 2 ) 2 1 i 0 e m = e ( ) i 0 In terms of the variable 0 , the function 1/( i ), is called a Complex Lorentzian. Its real and imaginary parts are: + + + + 1 1 i i i = = + 2 2 2 2 i i
Complex Lorentzian Real Imaginary + + + + 1 1 i i = = + i 2 2 2 2 i i 1/ Imaginary (even) component Real (odd) component 0
Okay, so weve determined what the light wave does to the atom. Now, what does the atom do to the light wave?
At every plane in the medium, light emitted from excited atoms interferes with the incident light beam. The resulting light then goes on to excite atoms in the next plane, where the same thing happens, etc., etc. What will be the light s field a distance z into the medium? Medium E(0,t) E(L,t) z L 0 So consider the total electric field: z E (z,t) = E incident(z,t) + Eemitted(z,t) Incident light + Emitted light Maxwell's Equations will allow us to solve for the total field, E (z,t). The incident field E (z = 0, t) will be the initial condition. = Transmitted light
The Inhomogeneous Wave Equation The induced polarization, P , is due to the medium: x where: 2 2 2 2 2 2 E 1 1 c 0 c E z z E t t P t E P ( ) t P = = = = ( ) ( ) t Re{ ( )} x t Nex t Ne ( ) P t P 0 0 2 2 0 2 2 2 t 2 2 2 e e where N = the electron number density. which defines , the susceptibility. 1 e m 0 E = P Ne E 0 2 ( ) i 0 0 e 2 2 2 1 c P t E t E t where c0 = the speed of light in vacuum = = 0 0 0 2 2 2 0 2 Substituting this into the inhomogeneous wave equation: + 2 2 2 2 2 1 c 1 c 1 E z E t E t E z E t = = 0 2 2 0 2 2 0 2 2 2 0 2 c