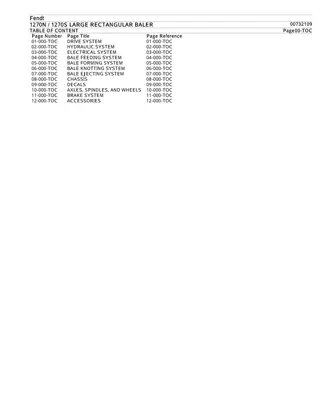
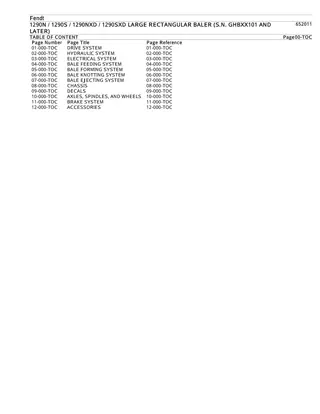
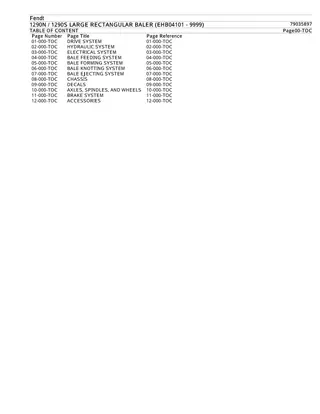
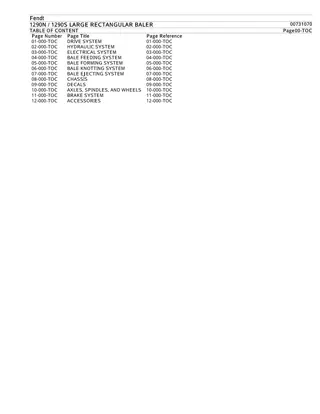
Rectangular Hyperbolas

Rectangular hyperbolas are a type of hyperbola with perpendicular asymptotes. Learn about their characteristics, asymptotes, dilations, and reflections in this informative content. Explore how horizontal and vertical asymptotes guide the shape of these graphs.

• Hyperbolas
• Asymptotes
• Dilations
• Reflections
• Graphs

brea_iah Follow

Uploaded on Feb 16, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Rectangular hyperbolas 4A

2. Rectangular hyperbola Consider the rule: ?=1 We can construct a table of values for ?= 1 ?=? 1 for ? 0 ?when 4 ? 4

3. Rectangular Hyperbolas A rectangular hyperbola is a hyperbola whose asymptotes are perpendicular. ?2 4 ?2 9= 1 Example: ?2 ?2= 1 The asymptotes of a hyperbola are not necessarily perpendicular In this chapter, you only need to know about rectangular hyperbola whose asymptotes are vertical and horizontal.

4. Asymptotes There are two lines associated with this graph that help to describe its shape. Horizontal asymptote Vertical asymptote

5. Horizontal asymptote From the graph we see that, as ? approaches infinity in either direction, the value of ? approaches zero. The following notation will be used to state this: As ? , ? 0+. This is read: As ? approaches infinity, ? approaches 0 from the positive side. As ? , ? 0 . This is read: As ? approaches negative infinity, ?approaches 0 from the negative side. The graph approaches the ?-axis (the line ?=0) but does not cross this line. The line ?=0 is a horizontal asymptote.

6. Vertical asymptote As ? approaches zero from either direction, the magnitude of ? becomes very large. The following notation will be used to state this: As ? 0+, ? . This is read: As ? approaches zero from the positive side, ?approaches infinity. As ? 0 , ? . This is read: As ? approaches zero from the negative side, ?approaches negative infinity. The graph approaches the ?-axis (the line ?=0) but does not cross this line. The line ?=0 is a vertical asymptote.

7. Dilations from an axis The graphs of 1 3 ? ?=1 The asymptotes: ?=0 & ?=0. The same shape & asymptotes, but stretched from ?=1 The transformation that takes the graph of ?=1 of ?=2 factor 2 from the ?-axis. Dilation: ?=1 ?, ?=2 ?and ?= 1 3?= ?. ?to the graph ?is called the dilation of ? ?=2 ?

8. Reflection in the ?-axis ?=1 the result is ?= 1 The asymptotes: ?=0 and ?=0. Similarly, ?= 2 reflection of ?= 2 Reflecting in the ?-axis gives the same result for these two graphs. ?is reflected in the ?-axis, ?. ?is the ?in the ?-axis.

9. Translations 1 The graph of ?= The basic graph of ?= 1 been translated 1 unit to the right and 3 units up. Asymptotes: ?=1& ?=3. Intercepts with the axes The graph now has ?-axis and ?-axis intercepts. ? 1+3. 3 units ?has 1 unit

10. Sketching rectangular hyperbolas Using dilations, reflections and translations, we are now able to sketch the graphs of all rectangular hyperbolas of the form ?= ? ? +k.

11. 2 Sketch the graph of ?= ?+1 3. The graph of ?= 2 translated 1unit and 3 units The asymptotes: ?= 1 & ?= 3. When ?=0, ?= the ?-axis intercept is 1. When ?=0, 0= ?has been 2 0+1 3 = 1. 2 ?+1 3 2 ?+1=3 3(?+1) =2 ?+1= 2 the ?-axis intercept is 1 3 ?= 1 3 3.

12. Sketch the graph of ?=2 ? 1. The graph of ?= 2 obtained from the graph of ?= 2 This graph is then translated 1 unit to obtain the graph of ?= 2 ?is ?by reflection in the ?-axis. ? 1.

13. Section summary For ?>0, a dilation of factor ? from the ?-axis transforms the graph of ?=1 A reflection in the ?-axis transforms the graph of ?=? the graph of ?= ? For , ? 0, a translation of to the right and ? upwards transforms the graph of ?= ? ? to the graph of ?=? ?. ? to ?. ? ? to the graph of ?= ? +?. ? ? +? A rectangular hyperbola with rule of the form ?= has: vertical asymptote ?= horizontal asymptote ?=?.

14. How to find a, h, k ? ?= ? +k. 1 3?+6 ? = 3*?+3*2=3(?+2) 1 3 1 1 3?+6 = 3(?+2) = ?+2 +0 ? = a= 1 3, h= 2, k=0

15. ? ?= ? +k. How to find a, h, k 3 2? ? 2= ( 3+2?) ? 2 (2? 3) ? 2 (2? 4+1) ? 2 2? 4 1 ? 2 = ? = = = 2(? 2) 1 ? 2 1 = 2 ? 2 = a= 1, h=2, k= 2