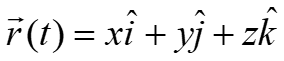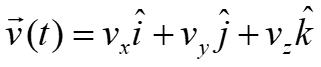Motion in Two and Three Dimensions

Concepts of motion in two and three dimensions, covering topics such as position vectors, displacement, velocity, and acceleration. Understand kinematics in different coordinate systems and solve displacement problems in multi-dimensional spaces. Practice writing position vectors for particles in rectangular coordinates and analyzing particle displacements in given scenarios.

• Motion
• Kinematics
• Position Vector
• Displacement
• Multi-dimensional

achip Follow

Uploaded on Feb 19, 2025 | 1 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Lecture 3 Motion in Two Dimensions and Three Dimensions Dr. Hind I. Al-Shaikh

2. Out lines of study Position Vector and Displacement Vector Average Velocity and Instantaneous Velocity Average Acceleration and Instantaneous Acceleration One dimensional motion with constant acceleration Relative Motion in Two Dimensions Motion in two dimensions with constant acceleration Projectile Motion Trajectory of Projectile Motion Horizontal range and maximum height of a projectile Projectile Motion Analyzed Uniform Circular Motion

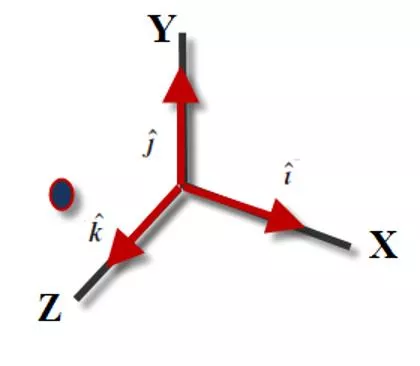
3. Position Vector and Displacement Vector Kinematics Displacement Velocity Acceleration (x,y,z Rectangular coordinate One general way of locating a particles with a position vector , which is a vector that extends from a reference point (usually the origin) to the particle. Kinematic variables in one dimension Position: x(t) m Velocity: v(t) m/s Acceleration: Kinematic variables in three dimensions Position: m Velocity: m/s Acceleration: k a j a i a t a z y x ) ( + + = x = = + + j ( ( ) ) r v t t i x v j y v + k z + k i v x y z All are vectors: have direction and magnitudes

4. Position and Displacement In one dimension = ( ) ( ) x x t x t 2 2 1 1 x1 (t1) = - 3.0 m, x2 (t2) = + 1.0 m x = +1.0 m + 3.0 m = +4.0 m = r r r 2 1 In two dimensions Position: the position of an object is described by its position vector always points to particle from origin. 1 Displacement: r (t ) = r r r 2 1 i ) ) 1 = + + ( ( r x y + j x i ) 1 y j 2 2 1 ) 1 = ( ( x x i y y j 2 2 = i x + j y

5. Position and Displacement in Three dimention Position vector: Displacement : Question 1: Write the position vector for a particale in the rectangular coordinate (x,y,z for points (5, -6, 0 , (5, -4 , and (-1, 3, 6 .

6. Question 1: Write the position vector for a particale in the rectangular coordinate (x,y,z for points (5, -6, 0 , (5, -4 , and (-1, 3, 6 . For the point 5,-6,0 the position vector For the point 5,-4 the position vector For the point -1, 3,6) the position vector

7. Question 2 : Displacement In Fig., the position vector for a particle is initiallyat and then later is 2r 1r to ? What is the particle's displacement from

8. Average & Instantaneous Velocity Instantaneous Velocity Average velocity Velocity . . The Average velocity of a particle is defined as the ratio of the displacement to the time interval. The unit of the velocity is The instantaneous Velocity of a particle is defined as the limit of the average velocity as the time interval approaches zero. v v t avg 0 0 t lim lim r r d = = t dt d r dx dy i j i j = = + = + v v v x y dt dt dt

9. Average & Instantaneous Acceleration AverageAcceleration Instantaneous Acceleration . Acceleration The average acceleration of particle is defined as the ratio of the change in the instantaneous velocity to the time interval. The unit of the acceleration is v aavg t v v i j i j y = + = + x a a a , , avg avg x avg y t t

10. The Instantaneous acceleration is defined as the limiting value of the ratio of the average velocity to the time interval as the time approaches zero. = dv dv v d v d v y = = + = + x a i j a i a j = lim lim a a avg x y t dt dt dt dt t 0 0 t The magnitude of the velocity (the speed) can change The direction of the velocity can change, even though the magnitude is constant Both the magnitude and the direction can change

11. Example A rabbit runs across a parking lot on which a set of coordinate axes has, strangely enough, been drawn. The coordinates of the rabbit s position as functions of time t (second) are given by A- At t = 15 s, what is the rabbit s position vector in unit vector notation and in magnitude-angle notation? B- What is the rabbit s velocity vector in unit-vector notation and in magnitude-angle notation? C- At t=15 s, what is the rabbit s acceleration vector in unit-vector notation and in magnitude-angle notation?

14. Summary in two dimension Position = + ) ( r t i x j y r x y = = + = ,+ v i j v i v j Average velocity , avg avg x avg y t t t dx dy Instantaneous velocity vx vy dt dx dt r r d dy = = = + = + ) ( lim v t i j i v v j x y t dt dt dt 0 t dv 2 2 dv d x d y Acceleration y = = x a a x y 2 2 dt dt dt dt dv dv v d v i j i j y = = = + = + ( ) lim x a t a a x y t dt dt dt 0 t ( , t v (t) r are not necessarily same direction. ), and ( ) a t

15. One Dimensional Motion with Constant Acceleration acceleration constant Instantaneous acceleration .Average acceleration . : Instantaneous acceleration Average acceleration =

16. Let then the acceleration or . . .

17. Eq. is true only for constant acceleration and with at the initial time . Also, since , we can integrate to get our second equation: Assuming . I often write this as:

18. What if we dont know t ? We can eliminate it by solving the first equation for t and putting it into the second equation: Changing the order of the terms gives us: To use these equation, we first identify the known and unknown quantities . . :

19. Example: Ali applies the brake in a car, starting at 100 km/hr and slowing to 80 km/hr in 88 m at a constant acceleration. A- What is ? B- How long did this take? Solution: First, identify knows and unknowns and convert ti SI units. knowns unknowns A- B-

20. Question: A body moving with uniform acceleration has a velocity of 12 cm/s when its x coordinate is 3 cm. If its x coordinate 2 s later is -5 cm, what is the magnitude of its acceleration?

21. Motion in two dimensions Motion in two dimensions like the motion of projectiles and satellites and the motion of charged particles in electric fields. Here we shall treat the motion in plane with constant acceleration and uniform circular motion. .

22. Motion in two dimensions with constant acceleration Assume that the magnitude and direction of the acceleration remain unchanged the motion. The position vector for a particle in two dimensions (x,y plane) can be written as: = + ( ) r t i x j y Where x, y and r change with tune as the particle moves the velocity of particle is given by:

23. Since the acceleration is constant then we can substitute t a v v x x x + = 0 v = + v a t 0 y y y This give Then .

24. Since our particle moves in two dimension x and y with constant acceleration then But Solve

25. Projectile Motion . 2-D problem and define a coordinate system: x- horizontal, y- vertical (up +) Try to pick x0 = 0, y0 = 0 at t = 0 Horizontal motion + Vertical motion Horizontal: ax = 0 , constant velocity motion Vertical: ay = -g = -9.8 m/s2, v0y = 0 Equations: Horizontal Vertical = + v v a t = + v v a t 0 = y y y 0 = x x x = + 2 y y v t 1gt f i iy 2 y+ 2 x+ y y v t a t 2 1 x x v t a t 1 0 0 y 2 0 0 + x 2 2 2 2 2 = = + 2 ( ) v v a x x 2 ( ) v v a y y 0 0 x x x 0 0 y y y

26. Projectile Motion 2-D problem and define a coordinate system. Horizontal: ax = 0 and vertical: ay = -g. Try to pick x0 = 0, y0 = 0 at t = 0. Velocity initial conditions: v0 can have x, y components. v0x is constant usually. v0y changes continuously. Equations: Horizontal = t v x x x 0 = vx= cos v v 0 0 0 vx= sin 0 0 0 Vertical v y = y = v gt v v 0 y 0 x x 0+ + y 2 y v t gt 1 0 0 2 February 5-8, 2013

27. Trajectory of Projectile Motion Initial conditions (t = 0): x0 = 0, y0 = 0 v0x = v0cos 0 and v0y = v0 sin 0 Horizontal motion: t v x 0 0 + = x = t x v Vertical motion: = 0 x + y y 2 0 y v t gt 1 0 x 2 2 g x = y v 0 2 v v 0 0 x x g = 2 tan y x x 0 2 2 2 cos v 0 0

28. Horizontal range and maximum height of a projectile The horizontal range R of the projectile is the horizontal distance the projectile has travelled when it returns to its initial height (the height at which it is launched). To find range h, let us put in eq. 1, and in eq. 2 .. 1 2 By substituting the time t in the above equation h . 90 or 45 . 3

29. Projectile Motion at Various Initial Angles 2 2 sin v Complementary values of the initial angle result in the same range The heights will be different The maximum range occurs at a projection angle of 45o = 0 R g

30. Example: A long jumper leaves the ground at an angle of 20 to the horizontal and a speed of 11 ms. A- How far does he jump? B- The maximum reached? A- X can be found if t is known from the equation =0.384 s where is the time required to reach the top then T=0.768 s Therefore x= 7.94 m B- The maximum height reached is found using the value of

31. Uniform Circular Motion linear constant speed . . . , , . . . .

32. Uniform Circular Motion Centripetal acceleration vi v = vf - vi v r v r = = so, vf v vi v r r y B A vf 2 v r v v = = r t t r r R ri rf 2 v v = = a r t r O x Direction: Centripetal

33. Uniform Circular Motion Velocity: Magnitude: constant v The direction of the velocity is tangent to the circle Acceleration: Magnitude: directed toward the center of the circle of motion Period: time interval required for one complete revolution of the particle ac v 2 v = ac r 2 v = ac r 2 r = T v

34. Summary Position = + ( ) r t i x j y r x y i j i j = = + = + v v v Average velocity , , avg avg x avg y t t t dx dy vx vy Instantaneous velocity dt dt r r d dx dy i j i j = = = + = + ( ) lim v t v v x y t dt dt dt 0 t 2 dv 2 dv d x d y = y = x a a Acceleration x y 2 2 dt dt dt dt dv dv v d v i j i j y = = = + = + ( ) lim x a t a a x y t dt dt dt 0 t , v (t) r are not necessarily in the same direction. ( ), and ( ) t a t

35. Summary If a particle moves with constant acceleration a, motion equations are v r r i f + = + 2 t 1t a i 2 i j ) ) = + = + + + + + 2 2 ( ( r x y x v t a t i y v t a t j 1 1 f f f i xi xi i yi yi 2 2 = + v v t a i i j ) ) = + = + + + ( ) ( ( v t v v v a t i v a t j f fx fy ix x iy y Projectile motion is one type of 2-D motion under constant acceleration, where ax = 0, ay = -g.

36. Question1 Figure shows a pirate ship 560 m from a fort defending a harbour entrance. A defense cannon, located at sea level, fires balls at initial speed v0 82 m/s. (a) At what angle u0 from the horizontal must a ball be fired to hit the ship? (b) What is the maximum range of the cannonballs?

37. Question2 A particle moves in a circular path 0.4m in radius with speed. If the particle makes five revolution in each second of its motion. Find a- the speed of the particle? b- its acceleration.