Maxwell's Equations and Spherical Currents
In the realm of physics, Maxwell's equations hold significant importance, especially in understanding the interplay between electricity and magnetism. Delve into the intricate concepts behind Gauss's laws, Faraday's law of induction, and Ampère's law in relation to spherical currents and magnetic fields. Explore the fascinating dynamics of electromagnetic phenomena and their theoretical underpinnings, shedding light on the fundamental principles governing these interactions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Maxwells Equations Physics 2415 Lecture 29 Michael Fowler, UVa
Todays Topics Maxwell s equations The speed of light
Equations for Electricity and Magnetism Gauss law for electric fields E dA = q / 0 the electric flux out of a volume = (charge inside)/ 0. Gauss law for magnetic fields B dA = 0 There is no such thing as magnetic charge: magnetic field lines just circulate, so for any volume they flow out of, they flow back into it somewhere else.
Equations for Electricity and Magnetism Electrostatics: (no changing fields) E d = 0 around any closed curve: this means the work done against the electric field from A to B is independent of path, the field is conservative: a potential energy can be defined. Faraday s law of induction: in the presence of a changing magnetic field, the above equation becomes: ( E d d dt B dA ) = = / / d dt B the integral is over an area roofing the path. A changing magnetic flux through the loop induces an emf.
Equations for Electricity and Magnetism Mangnetostatics: B d = I 0 around any closed curve: I is the total current flow across any surface roofing the closed curve of integration. But is this the whole story? Fields changing in time changed the electrostatic equation, what about this magnetostatic equation? Let s look at a particular case
Spherical Current At t = 0, a perfectly spherical ball of charge is placed at the center of a very large spherical conductor. The charge flows away equally in all directions. What is the magnetic field generated? 1) It points outwards equally in all directions 2) Same but pointing inwards 3) It circles around the initial sphere 4) No magnetic field is produced by these currents
Those Spherical Currents Cannot produce a magnetic field! The configuration has perfect spherical symmetry it would not be changed by turning it through an angle about any axis. The only fields satisfying this would point in or out along radii everywhere but that could only happen with a net magnetic charge (N or S) at the center. So, no field at all
Ampres Law and Spherical Currents Imagine in 3D currents flowing spherically outward symmetrically from a ball of charge injected into a large conducting medium. Imagine a circular curve, like a crown, placed above the source. Clearly some of the current flows through a surface roofing this loop, so 0I is nonzero. But around the loop, because the field B is zero everywhere! So Amp re s law is not the whole story B d = 0
Another Ampres Law Paradox Suppose now a capacitor is being charged by a steady current in a wire. Consider Amp re s law for a circular contour around the wire it s supposed to be the same for any surface S roofing the circle, but we could choose S2, going between the plates, so no current crosses it! I
Maxwells Solution Maxwell knew Faraday had generalized the electrostatic law to include a time-varying magnetic field by adding the changing flux through the curve: ( E d d dt ) = B dA = / / d dt B He noticed that when Amp re s law failed, there was a time-varying electric field through the surface roofing the curve, and suggested including it like this: ( 0 0 B d I E dA dt ) d = + = + / I d dt 0 0 0 E (Writing , the electric flux.) E dA = E
Why the Two Surfaces Give the Same Result The current I flowing through surface S1 is the rate of change of charge on the top capacitor plate, I = dQ/dt. If the plates are close, all the electric field from the top plate will point down, none will cross S1, so and I E dA = Q / 0 + S S 1 2 d d dt dQ dt E dA = = = I E 0 0 dt Bottom line: the rate of change of electric flux through S2 = current through S1. S 2
Ampres Law and Charge Conservation Amp re s law cannot work by itself for all surfaces spanning a circle like this: The surface S2 is drawn to avoid the current. This is only possible because charge is piling up. The rate of change of electric flux just equals times how fast the charge is piling up, from Gauss law. This must equal the ingoing current so the integral over S1 = that over S2. I 1/ 0
Maxwells Equations The four equations that together give a complete description of electric and magnetic fields are known as Maxwell s equations: E dA = q B dA = / 0 0 Maxwell himself called this term the displacement current : it produces magnetic field like a current. E d = / d dt B d B d = + I E 0 0 0 dt online notes
Magnetic Field In Charging Capacitor Taking the field between plates uniform, use . I d dt B d = + E d I A 0 0 0 For a disc surface between the plates, there is no current I through the surface, there is a changing electric field uniform over the area, generating a circular magnetic field. For the total plate area, d d dt dQ dt E dA = = = I E 0 0 dt
Magnetic Field In Charging Capacitor d dt dQ dt E dA = = For the total area I . 0 I For a disc of radius r, the total changing electric field is given by d E dA dt R 2 r R r = I 0 2 d dt = Now use B d E d A 0 0 I r = 0 B to find between plates. 2 R 2
Charging Capacitor and Betatron Recall that in the betatron a uniform magnetic field increasing in strength in time generated a circling electric field that could be used to accelerate charged particles. In the charging capacitor we ve been looking at, a uniform electric field increasing in strength in time generates a circling magnetic field. In regions of space where there are no charges, changing electric and magnetic fields are related to each other in a very symmetric way.
Clicker Question (Review) Suppose you have an infinite uniform plane of electric charge. What is its electric field? A. Parallel to the plane, of uniform strength. B. Parallel to the plane, decreasing strength with distance from the plane. C. Perpendicular to the plane, of uniform strength throughout space. D. Perpendicular to the plane, decreasing strength with distance from the plane.
Clicker Answer C: Perpendicular to the plane, of uniform strength throughout space. An infinite plane is of course an idealization: but for a uniform plane charge distribution of finite size, the electric field has very close to uniform strength for distances from the plane less than the linear size of the charge distribution.
Clicker Question Suppose now the uniformly charged plane is set in motion with constant velocity. This means we have a plane of electric current. The magnetic field generated by this current: A. Is perpendicular to the plane. B. Is parallel to the plane, and in the same direction as its velocity. C. Is parallel to the plane, and perpendicular to the velocity direction.
Clicker Answer Is parallel to the plane, and perpendicular to the velocity direction. Remember the Biot Savart law: The magnetic field from a small piece of current is perpendicular to the current direction but in this moving plane, all current flow is in the same direction, so all fields are perpendicular to that direction. r I d = 0 dB 2 4 r
Magnetostatic Field from a Sheet of Current (no net charge: current in metal sheet) A large uniform sheet of electric current: think of it as many parallel close wires perpendicular to the screen, current flowing downwards, I amps per meter. What is the magnetic field? There can be no perp field. It s OK to use Amp re s law with rectangular contour, the enclosed current is IL. . B-field L Infinite uniform current sheet: flows into screen B d = gives B = 0I/2. IL
Switching on the Current Sheet If the current sheet is suddenly switched on, in the first moments the magnetic field is only established close to the sheet. We ll assume it moves out like a tidal wave away from the sheet, at speed v, so at time t it extends out to vt, with nothing beyond. . (No B-field out here yet.) B-field Infinite uniform current sheet: flows into screen vt vt (No B-field out here yet.)
Ampres Law at Time t This rectangular contour still includes current LI, but clearly . What s going on? We know the correct equation is really B d LI = . (No B-field out here yet.) B d = 0 B-field vt vt + / d dt 0 0 0 E This will be correct only if there is also an electric field perpendicular to the loop, its flux increasing with time. (No B-field out here yet.)
Ampres Law at Time t As soon as the expanding magnetic field reaches our loop, and there can be no further change in the perpendicular electric field. This means the electric field E is spreading right along with the magnetic field, at v, so and from we find for field strengths . (No B-field out here yet.) B-field B d = LI 0 vt vt (No B-field out here yet.) = / 2 = = B d I = = + vE d dt EvL 0 B / LI d dt E 0 0 0 E / 2 0 0 0
Picturing the Fields The current sheet is in the xy-plane, current in the x direction. At time t after switch on, the fields will have reached vt as shown (we show one way fields go z too). We haven t yet used .x Electric field vt z Magnetic field y ( ) E d = B dA / d dt What does that tell us?
Picturing the Fields So let s look a . ( ) Electric field x E d = B dA / d dt Take a rectangular contour, two sides parallel to the electric field, one side beyond v: the integral gives . EL = vLB. (we re not worrying about sign these are field amplitudes.) vt L z Magnetic field y
The Speed of Light To summarize: for the outward traveling magnetic and electric fields from a switched-on current sheet, the equation B d LI = / 2 B I vE = = + / d dt 0 0 0 E gives . The equation gives E = vB. They both give the ratio B/E and that fixes v! 0 0 0 ( ) E d = B dA / d dt 1 v 1 B E = = = 3 10 m.sec = 8 1 , so v v 0 0 0 0
The Speed of Light This outgoing wave could have been made harmonic simply by oscillating the current in the sheet. The wave s outgoing speed is fully determined by 0, which remember we defined as 4 x10-7, and by 0, which is measured in electrostatic experiments. But the speed is exactly that of light! Maxwell concluded that light is an electromagnetic wave.
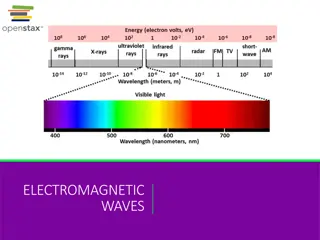
The Electromagnetic Spectrum The equations place no restriction on possible wavelengths of these electromagnetic waves. It follows that light, with wavelengths only between 400 nm and 750 nm, is a small part of a vast electromagnetic spectrum see the next slide