Integers, Divisibility, and Prime Numbers in Mathematics for Computer Science
Discover the fundamental concepts of integers, divisibility, remainder theorem, prime numbers, and their applications in computer science. Learn about integer division, examples of remainders, properties of divisibility, and the significance of prime numbers in cryptography. Explore the interplay between mathematics and computer science through practical examples and theoretical foundations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Lecture 6 Integers CSCI 1900 Mathematics for Computer Science Fall 2014 Bill Pine
Lecture Introduction Reading Rosen Section 4.1 Remainder Theorem Divisibility of integers Prime numbers GCD LCM Representing integers in different bases CSCI 1900 Lecture 6 - 2
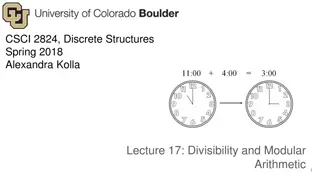
Remainder Theorem Given two integers, n and m with n> 0, Perform the integer division of m by n q is the quotient and r is the remainder q and r are unique because we require 0 <= r< n Therefore, we can write m=q*n + r This result is known as the Remainder Theorem CSCI 1900 Lecture 6 - 3
Examples of m = qn + r If n is 3 and m is 16 16 = 5*3 + 1 If n is 10 and m is 3 3 = 0*10 + 3 If n is 5 and m is 11 11 = 3*5 + 4 q = 5; r = 1 q = 0; r = 3 q = 3; r = 4 CSCI 1900 Lecture 6 - 4
Divisibility If one integer, n, divides into a second integer, m, without a remainder, then we say that n divides m Denoted n | m If one integer, n, does not divide evenly into a second integer, m, then we say that n does not divide m Denoted n | m CSCI 1900 Lecture 6 - 5
Some Properties of Divisibility If n | m, There exists an integer k such that m = k * n The absolute values of both k and n are less than the absolute value of m, i.e., |n| < |m| and |k| < |m| Examples: 4 | 24 24 = 4 * 6 both 4 and 6 are less than 24 5 | 135 135 = 5 * 27 both 5 and 27 are less than 135 CSCI 1900 Lecture 6 - 6
Simple properties of divisibility Given three integers a, b, c with a | b and a | c, then a | (b + c) a | (b - c) a | bc Given three integers a, b, c with a | b and b | c, then a | c CSCI 1900 Lecture 6 - 7
Prime Numbers A number p is called prime if the only positive integers that divide p are p and 1 Examples of prime numbers: 2, 3, 5, 7, 11 There are many computer algorithms that can be used to determine if a number n>1 is prime, with greater or lesser efficiency Who cares ? Anyone who buys anything online or has a wireless network they do not want to share ! Cryptography involves prime number in some manner CSCI 1900 Lecture 6 - 8
Basic Prime Number Algorithm Function IsPrime( n ) nIsPrime = True for i= 2 to n-1 if( i | n) nIsPrime = False Exit Loop return (nIsPrime) CSCI 1900 Lecture 6 - 9
Factoring a Number into its Primes Repeatedly dividing a number into its multiples until the multiples no longer can be divided, shows us that any number can be expressed a a product prime numbers Examples: 9 = 3 * 3 = 32 24 = 8 * 3 = 2 * 2 * 2 * 3 = 23 * 3 315 = 3*105 = 3*3*35 = 3*3*5*7 = 32 * 5 * 7 Any number can be expressed as a product of prime numbers This factorization is unique CSCI 1900 Lecture 6 - 10
Modulus The mod n operator is a direct consequence of the Remainder Theorem m mod n is defined to be the remainder when m is divided by n The divisor n is called the modulus Given m = q * n + r then we say m mod n = r If m mod n = 0 then m | n CSCI 1900 Lecture 6 - 11
Modulus(cont) Examples 13 mod 3 = 1 => 32 mod 5 = 2 => a mod 7 = 1 4*3+1=13 6*5+2=32 7*k+1=a, for some integer k => CSCI 1900 Lecture 6 - 12
Greatest Common Divisor If a, b, and c are in Z+, and c | a and c | b, we say that c is a common divisor of a and b If d is the largest such c, d is called the greatest common divisor (GCD) d is a multiple of every c, i.e., every c divides d If the GCD(a, b) = 1 then a and b are relatively prime CSCI 1900 Lecture 6 - 13
GCD Example Find the GCD of 540 and 315: First find the prime factors of each 540 = 22 * 33 * 5 315 = 32 *5* 7 540 and 315 share the divisors 3 and 5, 540 has 33 and 5 315 has 32 and 5 So each is equal 32 * 5 times some different primes So the largest is the GCD 32 * 5 = 45 315 45 = 7 and 540 45=12 CSCI 1900 Lecture 6 - 14
Euclids Algorithm Inputs: Output: two positive integers a and b, a > b gcd(a, b) the greatest common divisor of a and b Procedure: r=amodb while ( r> 0 ) a=b b=r r=amodb returnb CSCI 1900 Lecture 6 - 15
Euclids Algorithm Example For two integers a= 846 and b = 212 846 = 3 * 212 + 210 212 = 1 * 210 + 2 210 = 105 * 2 + 0 GCD=2 For two integers a= 555 and b = 296 555 = 1 * 296 + 259 296 = 1 * 259 + 37 259 = 7 * 37 + 0 GCD = 37 k1 = 3; r1 = 210 k2 = 1; r2 = 2 k3 = 105; r3 = 0 846 = 47 * 32 * 2 212 = 53 * 22 k1 = 1; r1 = 259 k2 = 1; r2 = 37 k3 = 7; r3 = 0 555 = 37 * 5 * 3 296 = 37 * 23 CSCI 1900 Lecture 6 - 16
Least Common Multiple If a, b, and k are in Z+, and a | k, b | k, we say that k is a common multiple of a and b The smallest such k, call it c, is called the least common multiple or LCM of a and b We write c = LCM(a, b) An important result is GCD(a, b)*LCM(a, b) = a*b This provides a convenient way to calculate LCM(a, b) CSCI 1900 Lecture 6 - 17
Representation of Integers In day-to-day life, we use decimal (base 10) arithmetic , but it is only one of many ways to express an integer value We say that a decimal value is the base 10 expansion of n or the decimal expansion of n If b > 1 is an integer, then every positive integer n can be uniquely expressed in the form: n = dkbk + dk-1bk-1 + dk-2bk-2+ + d1b1 + d0b0 where 0 < di< b, i = 0, 1, , k CSCI 1900 Lecture 6 - 18
Algorithm: Base 10 to Base b Input: two positive integers, base b and number n in base 10 Output: the value of n in base b Procedure: See Handout CSCI 1900 Lecture 6 - 19
Example: Decimal 482 to Base 5 482 = 96*5 + 2 96 = 19*5 + 1 19 = 3*5 + 4 3 = 0*5 + 3 48210 = 34125 (remainder (2) is d0 digit) (remainder (1) is d1 digit) (remainder (4) is d2 digit) (remainder (3) is d3 digit) CSCI 1900 Lecture 6 - 20
Example: Decimal 704 to Base 8 (Octal) 704 = 88*8 + 0 88 = 11*8 + 0 11 = 1*8 + 3 1 = 0*8 + 1 70410 = 13008 (remainder (0) is d0 digit) (remainder (0) is d1 digit) (remainder (3) is d2 digit) (remainder (1) is d3 digit) CSCI 1900 Lecture 6 - 21
Algorithm: Base b to Base 10 Input: two positive integers, base b and number n in base b Output: the value of n in base 10 Procedure: See Handout CSCI 1900 Lecture 6 - 22
Example: 32125 to Base 10 34125 = 3 * 53 + 4 * 52 + 1 * 51 + 2 * 50 = 3 * 125 + 4 * 25 + 1 * 5 + 2 * 1 = 375 + 100 + 5 + 2 = 48210 CSCI 1900 Lecture 6 - 23
Example: 13008 to Base 10 13008= 1 * 83 + 3 * 82 + 0 * 81 + 0 * 80 = 1 * 512 + 3 * 64 + 0 * 8 + 0 * 1 = 512 + 192 = 70410 CSCI 1900 Lecture 6 - 24
Nota Bene The two conversion algorithms are pairs If you convert a number n from base 10 to base b You can check your result by converting the result back to base 10 If you convert a number n from base b to base 10 You can check your result by converting the result back to base b CSCI 1900 Lecture 6 - 25
Key Concepts Summary Divisibility of integers Prime numbers Remainder Theorem GCD LCM Expansion into different base CSCI 1900 Lecture 6 - 26