Engendering Human Rights for Women's Empowerment
QCD effects in the muon
anomalous magnetic moment
LIP Internships 2021
André Nunes
Mário Amaro
Professor Gernot Eichmann
I
n
t
r
o
d
u
c
t
i
o
n
01
I
n
t
r
o
d
u
c
t
i
o
n
M
u
o
n
g
-
2
T
h
e
o
r
y
I
n
i
t
i
a
t
i
v
e
W
h
i
t
e
P
a
p
e
r
:
A
o
y
a
m
a
e
t
a
l
.
,
P
h
y
s
.
R
e
p
t
.
8
8
7
(
2
0
2
0
)
F
N
A
L
R
u
n
-
1
:
A
b
i
e
t
a
l
.
,
P
R
L
1
2
6
,
1
4
1
8
0
1
(
2
0
2
1
)
02
H
a
d
r
o
n
i
c
V
a
c
u
u
m
P
o
l
a
r
i
z
a
t
i
o
n
(
H
V
P
)
03
Q
u
a
r
k
p
r
o
p
a
g
a
t
o
r
●
Free particle:
●
"Dressed” quark (spin ½ )
●
Quark mass becomes large at
small momenta (spontaneous chiral
symmetry breaking)
04
●
Spontaneous chiral symmetry breaking is non-perturbative
●
Quark Dyson-Schwinger Equation (DSE):
Q
u
a
r
k
p
r
o
p
a
g
a
t
o
r
05
Q
u
a
r
k
-
p
h
o
t
o
n
v
e
r
t
e
x
●
Quark-photon vertex describes the electromagnetic coupling of quarks
to photons
B
e
t
h
e
-
S
a
l
p
e
t
e
r
E
q
u
a
t
i
o
n
s
(
B
S
E
)
06
Q
u
a
r
k
-
p
h
o
t
o
n
v
e
r
t
e
x
(
p
r
a
c
t
i
c
e
)
●
Start with an orthonormal basis
●
Chebyshev polynomials
●
Change to {g, f} basis07
H
a
d
r
o
n
i
c
v
a
c
u
u
m
p
o
l
a
r
i
z
a
t
i
o
n
08
H
a
d
r
o
n
i
c
v
a
c
u
u
m
p
o
l
a
r
i
z
a
t
i
o
n
09
A
n
o
m
a
l
o
u
s
m
a
g
n
e
t
i
c
m
o
m
e
n
t
●
Having calculated all ingredients, we finally obtain:
10
R
e
s
u
l
t
s
a
n
d
D
i
s
c
u
s
s
i
o
n
11
The exploration of gendered poverty, the role of law in perpetuating inequalities, and interlocking factors affecting women's rights and opportunities. Addressing issues such as early marriage, lack of education, violence, and precarious work, highlighting the need for an engendered approach to human rights for sustainable development.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
QCD effects in the muon anomalous magnetic moment LIP Internships 2021 Andr Nunes M rio Amaro Professor Gernot Eichmann
Introduction Muon has spin , so it has a magnetic moment ( g factor ), encoded in electromagnetic coupling of the photon to the muon g=2 for a pointlike particle Anomalous magnetic moment ( g-2 or ??= (g-2)/2 ) comes from quantum effects (tiny): ??= 0.00116 Experiments at BNL, Fermilab (run 1 2021), JPARC (future) 01
Introduction Muon g-2 Theory Initiative White Paper: Aoyama et al., Phys. Rept. 887 (2020) FNAL Run-1: Abi et al., PRL 126, 141801 (2021) 02
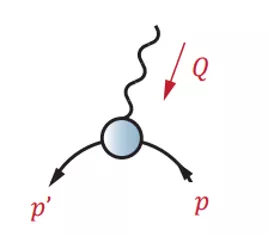
Hadronic Vacuum Polarization (HVP) Biggest QCD contribution, contributes main uncertainty in SM prediction Different ways to calculate ? employed in literature; here: alternative method ??? Two ingredients: quark propagator and quark-photon vertex 03
Quark propagator Free particle: "Dressed quark (spin ) Quark mass becomes large at small momenta (spontaneous chiral symmetry breaking) 04
Quark propagator Spontaneous chiral symmetry breaking is non-perturbative Quark Dyson-Schwinger Equation (DSE): ? ? = 1 + ??(?) 05
Quark-photon vertex Quark-photon vertex describes the electromagnetic coupling of quarks to photons Bethe-Salpeter Equations (BSE) 06
Quark-photon vertex (practice) Start with an orthonormal basis Chebyshev polynomials Change to {g, f} basis 07
Hadronic vacuum polarization We need to fit a quadratic function for small ?2: 09
Anomalous magnetic moment Having calculated all ingredients, we finally obtain: 10
Results and Discussion ???(u, d) + ? ???(s) + ? ???(c) ? = 768(21) x10 10 ... if scale adjusted to ? = 711(21) x10 10 if scale adjusted to ? meson (errors are model uncertainties) Somewhat larger than current SM prediction Need to increase precision, test sensitivity to fits, etc. 11
