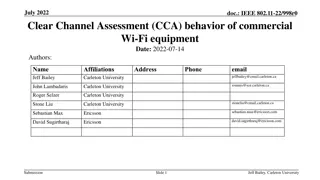
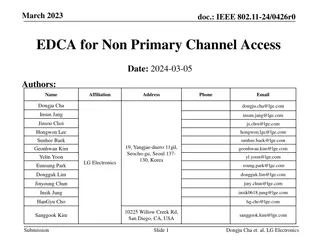
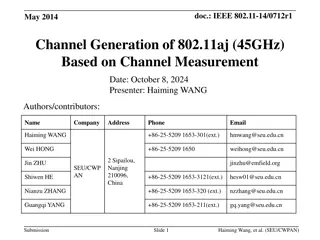
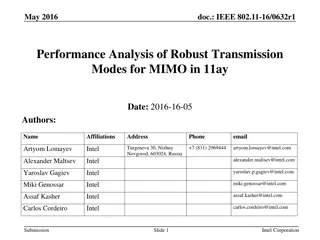
Channel Estimation for OTFS Massive MIMO
Explore the channel estimation techniques for Orthogonal Time Frequency Space (OTFS) in Massive MIMO systems, focusing on system models, OTFS SISO modulation and demodulation, and the input-output relation lemma. Learn about key concepts such as delay-Doppler-angle 3D channel and simulation results. Discover how OTFS modulation and demodulation are implemented, along with the mapping between delay-Doppler and frequency-time domains.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO BEIJING INSTITUTE OF TECHNOLOGY BEIJING INSTITUTE OF TECHNOLOGY 1Wenqian Shen, 2Linglong Dai, 3Shuangfeng Han, 3Chih-Lin I, and 4Robert W. Heath, Jr. 1School of Information and Electronics, Beijing Institute of Technology 2Department of Electronic Engineering, Tsinghua University 3Green Communication Research Center, China Mobile Research Institute 4Department of Electrical and Computer Engineering, The University of Texas at Austin 1/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Outlines System Model 1. 2. Delay-Doppler-Angle 3D Channel 3D-SOMP Based Channel Estimation 3. 4. Simulation Results 2/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
OTFS SISO Modulation OTFS modulation at the transmitter is composed of an OTFS pre-processing block and a traditional frequency-time modulator such as OFDM. The OTFS pre-processing block maps the 2D data block in the delay-Doppler domain to the 2D block in the frequency-time domain by using the inverse symplectic finite Fourier transform (ISFFT). M N X DD X FT M N = s A S A S FT DD ISFFT vec{ } X X X S CP CP ( ) Transmit Windowing Parallel to Serial M-point IDFT ( ) + + M N N M N 1 M N N Input M N M N M N ISFFT Add CP CP CP OTFS Pre-processing OFDM Modulator 3/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
OTFS SISO Demodulation OTFS demodulation at the receiver is composed of the traditional OFDM demodulator and an OTFS post-processing block. The OTFS post-processing block maps the received signals in the frequency-time domain to the 2D block in the delay-Doppler domain by using the SFFT. Y Y Y M N FT Y M N DD Y r = R R R r unvec{ } FT FT,W DD CP ( ) + M N N Output ( ) CP Remove CP Serial to Parallel M-point DFT Equaliza tion Receive Windowing + 1 M N N M N M N M N M N M N CP SFFT OTFS Post-processing OFDM Demodulator Channel Estimation 4/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
OTFS Input-Output Relation Lemma 1: The received data compensated 2D periodic convolution of the transmit data with the delay-Doppler channel impulse response (CIR) H is given by the phase DD Y DD X , which is shown as follows: M N DD N 1 1 M l = 2 N + DD , k DD , DD l l DD , k , Y X H w V k k k k l l , l , l k = N 0 = k 2 ( l ) where , , and are the -th element of YD , , and ( , ). 0,1, , = l L X Y H + + + DD ,k DD ,k DD ,k 1, 1 / 2 Hl Xl Yl k N DD DD DD = 1 / 2, ,0, , L L / 2 1 M k N N k N N 2 ( 1) j i = DD , k H h e 1)( M N + ) 1,( ) + Time-variant CIR l ( l i CP M = 1 i h l , 5/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
OTFS Massive MIMO OTFS working in massive MIMO systems can further increase the spectrum efficiency by using multi-user MIMO. The main challenge for OTFS massive MIMO is the downlink channel estimation due to the required high pilot overhead. Channel Estimation r TF , n m Y DD , kYl s DD , k TF , n m X X l Resource Element Mapping Demodulator Time- frequency Output OTFS OTFS Pre- processing Block Time- frequency Modulator Modulator Time- frequency Demapping Equalization OTFS Post-processing Mapping Pre-processing OTFS Demodulation User 1 OTFS Modulation Input Precoding s DD , k TF , n m X X Channel Estimation l Time- frequency Modulator OTFS r Mapping TF , n m Y DD , kYl Pre-processing Resource Element Mapping Demodulator Time- frequency Output OTFS Modulation OTFS Antenna Ports Demapping Equalization Post-processing Base Station OTFS Demodulation User U 6/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Delay-Doppler-angle 3D Channel p+ The time-variant CIR associated with the -th antenna can be expressed as N N j p s i s = = ( 1) p s 2 2 T j p = p ( l ) , h e T e s s s i i , , l rc s i i 1 1 i Path gain Doppler frequency Time delay Spatial AoD Then, the delay-Doppler-angle 3D channel is given by ( 1 1 s i i ) N N p s ( ) p ( ) l ( ) NT k T r N = DDA , , k r , H rc s t s N s M i N s l t i i i = = sin( sin( ) x = ( 1) / j N x N ( ) x e N x N / ) 7/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
3D Sparsity of Delay-Doppler-angle Channel The 3D channel is sparse along the delay dimension, block-sparse along the Doppler dimension, and burst-sparse along the angle dimension. Delay Doppler Angle 8/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Training pilots in the delay-Doppler Domain To reduce the overall pilot overhead in OTFS massive MIMO systems, we propose the non- orthogonal pilot pattern, i.e., pilots transmitted at different antennas completely overlap. Data Pilot Guard The training sequences at different antennas are independently generated / 2 / 2 N N N g g g M Delay (M) M g M Doppler (N) 9/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Formulation of OTFS Channel Estimation Based on the OTFS input-output relation, the received pilots can be expressed as DFT of the transmit pilots N N g t 1 1 1 M 2 l 2 g = + DDA , , k r y w H z v k k r l , l l , l l l , , l , k k k = N N 0 t g = = r k 2 2 Rewrite it into the vector-matrix form as = + y h v This is a sparse signal recovery problem. 10/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
3D-SOMP Algorithm Reshape the correlations as the same size of the 3D channel matrix The delay index of the ?-th dominant path The Doppler support of the ?-th dominant path Transform the burst-sparsity to the block-sparsity and obtain the angle support of the ?-th dominant path 11/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Simulation Results For comparison, we also simulate the traditional impulse-based channel estimation method and traditional OMP-based channel estimation method. System parameters for simulations: 12/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Simulation Results NMSE vs. Pilot overhead 0 10 Traditional impulse based technique Traditional OMP based technique Proposed 3D-SOMP based technique NMSE -1 10 -2 10 0.2 0.25 0.3 0.35 Pilot overhead ratio ( ) 0.4 0.45 0.5 0.55 0.6 To achieve a constant NMSE, the required pilot overhead of the proposed method is smaller than that of its traditional counterparts. 13/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Simulation Results NMSE vs. # of BS antennas 1 10 Traditional impulse based technique Traditional OMP based technique Proposed 3D-SOMP based technique 0 10 NMSE -1 10 -2 10 10 20 30 40 50 60 Number of BS antennas (Nt) The proposed method works well with a large number of BS antennas. 14/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Simulation Results BER vs. SNR 0 10 -1 10 -2 10 BER -3 10 OFDM under ICI OFDM with perfect CSI OTFS with Impulse OTFS with 3D-SOMP OTFS with perfect CSI -4 10 0 5 10 15 20 25 30 SNR The proposed method achieves satisfying BER performance, which is very close to the case with perfect CSI in OTFS systems. 15/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Conclusions Show the 3D sparsity of delay-Doppler- angle channel Doppler Derive the discrete-time formulation of OTFS modulation/demodulation Delay N 1 1 M l = 2 N + DD , k DD , DD l l DD , k , Y X H w V k k k k l l , l , l k Angle = N 0 = k 2 1 10 Propose a 3D-SOMP algorithm for channel estimation in OTFS massive MIMO systems Traditional impulse based technique Traditional OMP based technique Proposed 3D-SOMP based technique 0 10 NMSE -1 10 -2 10 10 20 30 40 50 60 Number of BS antennas (Nt) 16/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO
Contact Information Thank you for your attention ! Wenqian Shen Beijing Institute of Technology wshen@bit.edu.cn http://oa.ee.tsinghua.edu.cn/dailinglong/members/wenqianshen 17/17 IEEE ICC 2019 Channel Estimation for Orthogonal Time Frequency Space (OTFS) Massive MIMO