Analysis of Various Arch Structures and Applications
Explore the design and behavior of different arch types such as extrados, intrados, two-hinged arch, three-hinged arch, tied arch, and parabolic arches. Solutions for loaded arch examples are provided, demonstrating reactions, tension calculations, and axial compression analysis. The content details how components are determined using equations based on structural mechanics principles.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
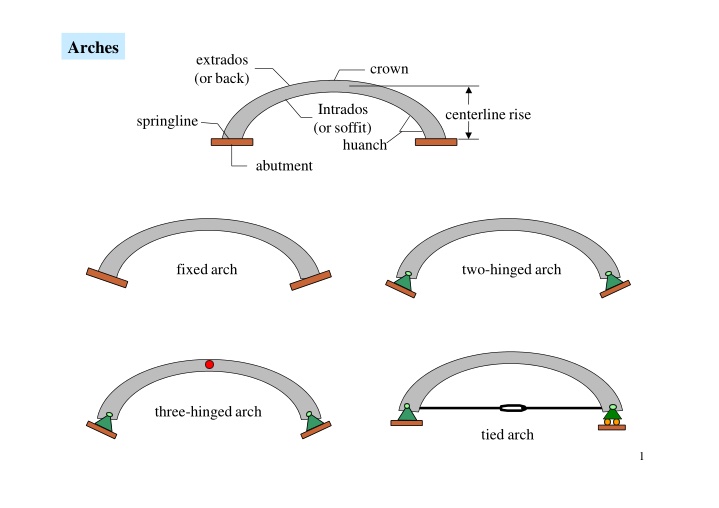
Arches extrados (or back) crown Intrados (orsoffit) centerline rise springline huanch abutment fixedarch two-hingedarch three-hingedarch tied arch 1
Three-Hinged Arch P1 C P2 D B A P1 MD C ND Cx Cy D VD C Cy A Cx x Ax P2 A Bx Ay Ay B By 2
Example 5-8 The tied three-hinged arch is subjected to the loading shown. Determine the components of reaction at A and C and the tension in the cable. 15 kN B 10 kN 2 m A D C 2 m 2 m 0.5 m 1 m 3
SOLUTION 15 kN B 10 kN 2 m A Ax D 0 C Ay 2 m 2 m Cy 0.5 m 1 m Entire arch : Cy(5.5) 10(4.5) 15(0.5) = 0 + MA= 0: Cy= 9.545 kN Ay 15 10+9.545 = 0 Fy= 0: + Ay= 15.46 kN 40
15 kN B B Bx Bx 10 kN By By 2 m A TA D TD Ay= 15.46 kN C Cy= 9.545 kN 2 m 2 m 0.5m 1 m MemberAB : 15(2) 15.455(2.5)+TA(2) = 0 + MB= 0: TA= 4.319 kN 15.455 15 By= 0 Fy= 0: By= 0.455 kN + + Fx= 0: 4.319 Bx= 0 Bx= 4.319 kN MemberAB : + Fx= 0: 4.319 TD= 0 TD= 4.319 kN 41
Example 5-6 The three-hinged open-spandrel arch bridge shown in the figure below has a parabolic shape and supports the uniform load . Show that the parabolic arch is subjected only to axial compression at an intermediate point D along its axis. Assume the load is uniformly transmitted to the arch ribs. y 7 kN/m x B y = 7.5x2 D 7.5m A C (15)2 15 m 7.5 m 7.5m 6
SOLUTION 210 kN B y = 7.5x2 Ax Cx (15)2 Ay Cy 15 m 15 m Entire arch : Cy(30) 210(15) = 0 + MA= 0: Cy= 105 kN Ay 210+105 = 0 Fy= 0: + Ay= 105 kN 7
105 kN B Bx By Cx B 105 kN 7.5 m 7.5 m Arch segment BC : 105(7.5)+105(15) Cx(7.5) = 0 + MB= 0: Cx= 105 kN + Bx= 105 kN Fx= 0: By 105+105 = 0 Fy= 0: + By= 0 8
52.5kN B 105 kN MD 26.6o ND D 0 VD 26.6o 3.75 m Arch segment BD : A section of the arch taken through point D, x = 7.5 m, y = -7.5(7.52)/(15)2= -1.875 m, is shown in the figure. The slope of the segment at D is 15x tan =dy= = 26.6o = 0.5, (15)2 dx x=7.5 + Fx= 0: Fy= 0: 105 - NDcos 26.6o- VDsin 26.6o= 0 -52.5 + NDsin 26.6o- VDcos 26.6o= 0 + + MD= 0: MD+ 52.5(3.75) - 105(1.875) = 0 ND= 117.40 kN, VD= 0, MD= 0 kN 31
52.5kN Alternate Method B 105 kN MD 26.6o ND D 0 VD 26.6o 3.75 m Arch segment BD : A section of the arch taken through point D, x = 7.5 m, y = -7.5(7.52)/(15)2= -1.875 m, is shown in the figure. The slope of the segment at D is 15x tan =dy= = 26.6o = 0.5, x=7.5 (15)2 dx ND 7.5 w = (7.5)(7)= 52.5 kN o =T = E (105)2+(52.5)2 No= 25 kN T max Notes : Since the arch is a parabola, there are no shear and bending moment, only NDis present 32 Tmax= 117.4 kN













![Legal Dispute Analysis: FCA v ARCH and Others [2021] UKSC 1](/thumb/189783/legal-dispute-analysis-fca-v-arch-and-others-2021-uksc-1.jpg)