Understanding Expander Families and Ramanujan Graphs
An introduction to expander families and Ramanujan graphs by Tony Shaheen from CSU Los Angeles. The discussion covers the concept of regular graphs, motivation behind expander families, communication networks, and the goal of creating an infinite sequence of d-regular graphs optimized for communicat
0 views • 54 slides
Exploring Product and Knowledge Graphs for Enhanced Information Retrieval
Dive into the world of product and knowledge graphs, uncovering the journey to a rich product graph, examples of knowledge graphs for songs, and the mission to provide comprehensive information on products and related knowledge. Discover use cases ranging from information provision to enhancing sear
3 views • 76 slides
Understanding Laplace Interpolation for Sparse Data Restoration
Laplace Interpolation is a method used in CSE 5400 by Joy Moore for interpolating sparse data points. It involves concepts such as the mean value property, handling boundary conditions, and using the A-times method. The process replaces missing data points with a designated value and approximates in
1 views • 13 slides
Physics Clicker Questions and Graphs
Explore a set of physics clicker questions and accompanying graphs covering topics such as ball motion, light refraction, Moon phases, velocity graphs, and integration methods. Test your knowledge and understanding of physics concepts with these engaging questions.
2 views • 17 slides
Exploring Various Types of Graphs in Statistics Education
Delve into the world of data visualization with slow reveal graphs, column graphs, pictographs, dot plots, divided bar graphs, sector graphs, line graphs, and stem-and-leaf plots. Engage in observations and wonderings to enhance statistical comprehension and analytical skills.
1 views • 8 slides
Understanding Bellman-Ford and Dynamic Programming on Graphs
Exploring Bellman-Ford and Floyd-Warshall algorithms, Dijkstra's Algorithm, shortest path problems, dynamic programming on graphs, and solving distances in a directed acyclic graph. Learn about recurrences, evaluation orders, topological sort, and handling cycles in graphs.
1 views • 39 slides
National 5 Applications of Maths: Charts, Graphs, and Tables Examples
Explore various examples related to reading bar charts, line graphs, stem-and-leaf diagrams, pie charts, and constructing stem-and-leaf charts in the context of National 5 Applications of Maths. Practice interpreting data from tables, line graphs, and stem-and-leaf diagrams to enhance your understan
0 views • 18 slides
Exploring Graphs: An Introduction to Data Visualization
This chapter delves into various types of graphs used in data representation, such as bar graphs, pie graphs, histograms, line graphs, and linear graphs. It explains the purpose and structure of each graph type, along with practical examples. Additionally, it covers the Cartesian system for locating
0 views • 15 slides
Understanding Functions and Graphs in Mathematics
Functions are a fundamental concept in mathematics used to describe relationships in the real world. They can be represented through equations, graphs, tables, or verbal descriptions. A function maps elements from a domain to a range, where each input has a unique output. The domain encompasses all
0 views • 4 slides
Understanding Bar Graphs, Double Bar Graphs, and Histograms
Bar graphs are useful for displaying and comparing data, while double bar graphs help compare two related datasets. Histograms show the distribution of data. Learn how to interpret and create these visual representations effectively with examples provided.
0 views • 20 slides
Primal-Dual Algorithms for Node-Weighted Network Design in Planar Graphs
This research explores primal-dual algorithms for node-weighted network design in planar graphs, focusing on feedback vertex set problems, flavors and toppings of FVS, FVS in general graphs, and FVS in planar graphs. The study delves into NP-hard problems, approximation algorithms, and previous rela
0 views • 17 slides
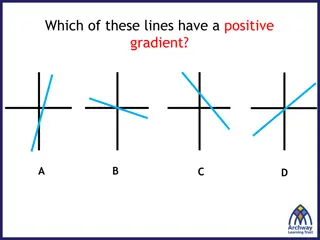
Understanding Graphs of Straight Lines and Equations
Learn how to graph equations and find equations from graphs of straight lines. Explore tables of values, plotting points on a coordinate plane, drawing lines through points, and identifying relationships between graphs and algebraic expressions. Discover the gradient-intercept form of a straight lin
0 views • 14 slides
Understanding Speed vs. Time Graphs: Analyzing Acceleration and Motion
Explore the concept of speed vs. time graphs and learn how to recognize acceleration, interpret speed, analyze motion, and calculate acceleration from the slope of the graph. Discover the characteristics of graphs showing constant acceleration, varying acceleration, and deceleration. Engage in drawi
0 views • 19 slides
Noise Sensitivity in Sparse Random Matrix's Top Eigenvector Analysis
Understanding the noise sensitivity of the top eigenvector in sparse random matrices through resampling procedures, exploring the threshold phenomenon and related works. Results highlight the impact of noise on the eigenvector's stability and reliability in statistical analysis.
0 views • 7 slides
Understanding Sparse vs. Dense Vector Representations in Natural Language Processing
Tf-idf and PPMI are sparse representations, while alternative dense vectors offer shorter lengths with non-zero elements. Dense vectors may generalize better and capture synonymy effectively compared to sparse ones. Learn about dense embeddings like Word2vec, Fasttext, and Glove, which provide effic
0 views • 44 slides
Overview of Sparse Linear Solvers and Gaussian Elimination
Exploring Sparse Linear Solvers and Gaussian Elimination methods in solving systems of linear equations, emphasizing strategies, numerical stability considerations, and the unique approach of Sparse Gaussian Elimination. Topics include iterative and direct methods, factorization, matrix-vector multi
0 views • 35 slides
Representation of Abstract Groups through Graphs
Explore the representation of abstract groups as automorphism groups of graphs, touching on topics such as the existence of graphs whose automorphism groups are isomorphic to given abstract groups, the cardinality of connected graphs satisfying specific properties, and questions regarding the cardin
0 views • 16 slides
Understanding Low Threshold Rank Graphs and Their Structural Properties
Explore the intriguing world of low threshold rank graphs and their structural properties, including spectral graph theory, Cheeger's inequality, and generalizations to higher eigenvalues. Learn about the concept of threshold rank, partitioning of graphs, diameter limits, and eigenvectors approximat
0 views • 22 slides
Exploring Types of Graphs for Data Representation
Different types of graphs, such as line graphs, scatter plots, histograms, box plots, bar graphs, and pie charts, offer diverse ways to represent data effectively. Understanding when to use each type based on the data being collected is essential for insightful analysis. Scatter plots are ideal for
2 views • 37 slides
Exploring Relationships Through Graphs
Learn how to analyze and relate two quantities using graphs, analyze data presented in tables and graphs, and sketch graphs representing various scenarios such as the movement of a model rocket or a playground swing. The visuals provided will help you understand how to interpret and draw graphs in d
2 views • 7 slides
Dynamic Load Balancing in Block-Sparse Tensor Contractions
This paper discusses load balancing algorithms for block-sparse tensor contractions, focusing on dynamic load balancing challenges and implementation strategies. It explores the use of Global Arrays (GA), performance experiments, Inspector/Executor design, and dynamic buckets implementation to optim
1 views • 32 slides
Threaded Construction and Fill of Tpetra Sparse Linear System Using Kokkos
Tpetra, a parallel sparse linear algebra library, provides advantages like solving problems with over 2 billion unknowns and performance portability. The fill process in Tpetra was not thread-scalable, but it is being addressed using the Kokkos programming model. By utilizing Kokkos data structures
0 views • 19 slides
Understanding Correlation in Scatter Graphs
In this content, various graphs are used to demonstrate the concept of correlation in scatter graphs. It discusses positive, negative, and no correlation, showcasing how one variable affects the other. Examples and explanations are provided to help understand the relationships between different sets
0 views • 17 slides
Statistical Dependencies in Sparse Representations: Exploitation & Applications
Explore how to exploit statistical dependencies in sparse representations through joint work by Michael Elad, Tomer Faktor, and Yonina Eldar. The research delves into practical pursuit algorithms using the Boltzmann Machine, highlighting motivations, basics, and practical steps for adaptive recovery
0 views • 47 slides
Symmetric Chromatic Function for Voltage Graphs
Exploring the concept of a Symmetric Chromatic Function (SCF) for voltage graphs involves proper coloring conditions for edges and vertices, edge polarization functions, and decomposing voltage graphs into disconnected and connected squiggly graphs. The SCF allows for determining the number of ways
0 views • 7 slides
Efficient Coherence Tracking in Many-core Systems Using Sparse Directories
This research focuses on utilizing tiny, sparse directories for efficient coherence tracking in many-core systems. By optimizing directory entries and leveraging sharing patterns, the proposed approach achieves high performance with minimal on-chip area investment. Results demonstrate significant en
0 views • 66 slides
Uniquely Bipancyclic Graphs by Zach Walsh
Research conducted at the University of West Georgia focused on uniquely bipancyclic graphs, defined as bipartite graphs with exactly one cycle of specific lengths determined by the order. Uniquely bipancyclic graphs have special properties, including having a Hamiltonian cycle and a specific order
0 views • 18 slides
Communication Costs in Distributed Sparse Tensor Factorization on Multi-GPU Systems
This research paper presented an evaluation of communication costs for distributed sparse tensor factorization on multi-GPU systems. It discussed the background of tensors, tensor factorization methods like CP-ALS, and communication requirements in RefacTo. The motivation highlighted the dominance o
0 views • 34 slides
Understanding Graphs for Mathematical Interpretation
Explore how students can grasp information through graphical formats and convert it into mathematical graphs. Learn about qualitative graphs, functions, axes, and more. Delve into exercises matching graphs with situations and drawing graphs for given scenarios like plane take-off, biking, and snowbo
0 views • 16 slides
Understanding Batch Estimation and Solving Sparse Linear Systems
Explore the concepts of batch estimation, solving sparse linear systems, and Square Root Filters in the context of information and square-root form. Learn about extended information filters, information filter motion updates, measurement updates, factor graph optimization, and more. Understand how S
0 views • 37 slides
Graph Property Testing and Algorithms Overview
Explore testable bounded degree graph properties, sparse graphs, d-bounded degree graphs, hyperfinite graphs, arboricity, maximum matching algorithms, and sublinear time approximation algorithms in graph data streams. Learn about various graph models and properties with examples, showcasing the impo
0 views • 53 slides
Exploring Efficient Hardware Architectures for Deep Neural Network Processing
Discover new hardware architectures designed for efficient deep neural network processing, including SCNN accelerators for compressed-sparse Convolutional Neural Networks. Learn about convolution operations, memory size versus access energy, dataflow decisions for reuse, and Planar Tiled-Input Stati
0 views • 23 slides
Adjacency Labeling Schemes and Induced-Universal Graphs
Adjacency labeling schemes involve assigning L-bit labels to vertices in a graph for efficient edge determination. The concept of induced-universal graphs is explored, where a graph is universal for a family F if all graphs in F are subgraphs of it. Theorems and lower bounds related to adjacency lab
0 views • 24 slides
Understanding Kinematics Graphs in Physics
Explore the concepts of kinematics graphs through diagrams and descriptions. Learn to interpret distance-time, velocity-time, and speed-time graphs. Understand key parameters such as displacement, initial velocity, final velocity, constant acceleration, and time spent on different parts of a journey
0 views • 33 slides
Understanding Graphs and Their Models
Explore the world of graphs through definitions, types, and special features. Learn about vertices, edges, simple and multiple graphs, directed and undirected graphs, and more. Discover the terminology and special types of graphs along with basic concepts and properties.
0 views • 33 slides
Introduction to Graph Theory: Exploring Graphs and Their Properties
This content delves into the realm of graph theory, focusing on the fundamental concepts and applications of graphs. It covers topics such as the Seven Bridges of Königsberg problem, types of graphs, vertex degrees, degree sequences, handshaking theorem, and more. Through visual aids and explanatio
0 views • 71 slides
Understanding Directed Graphs and Adjacency Matrices in Discrete Structures
Explore the concepts of binary relations, directed graphs, adjacency matrices, transitive closure, and walks in the context of discrete structures. Learn how vertices, edges, in-degrees, out-degrees, and self-loops are defined in directed graphs. Understand the importance of adjacency matrices in re
0 views • 28 slides
Understanding Graphs in Mathematics and Computer Science
Graphs in mathematics and computer science are abstract data types used to represent relationships between objects. They consist of vertices connected by edges, which can be directed or undirected. Graphs find applications in various fields like electric circuits, networks, and transportation system
0 views • 19 slides
Understanding Graphs in Discrete Mathematics
Graphs are fundamental objects in discrete mathematics that model relationships between pairs of objects. This overview covers the vocabulary, formal definitions, and types of graphs, including directed and undirected graphs. Learn about vertices, edges, adjacency, and more essential concepts in gra
0 views • 18 slides
Orthogonal Vectors Conjecture and Sparse Graph Properties Workshop
Exploring the computational complexity of low-polynomial-time problems, this workshop delves into the Orthogonal Vectors Problem and its conjectures. It introduces concepts like the Sparse OV Problem, first-order graph properties, and model checking in graphs. Discussing the hardness of problems rel
2 views • 22 slides