Inductive calculus - PowerPoint PPT Presentation

Dental calculus, also known as tartar, is a mineralized bacterial plaque that forms on natural teeth and dental prostheses. It can be classified as supragingival or subgingival based on its relation to the gingival margin. This hard deposit is formed through the mineralization of dental plaque and c

10 views • 36 slides

Explore various calculus problems involving finding gradients, equations of tangents and normals, and analyzing curves. Practice determining gradients at specific points, solving for coordinates, and differentiating equations to find tangent and normal lines. Understand the relationship between grad

4 views • 11 slides

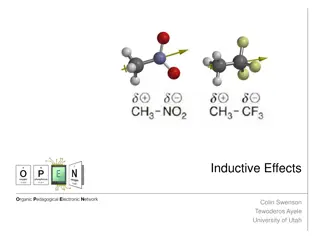
Inductive effects play a crucial role in the reactivity and properties of organic molecules. This phenomenon involves the withdrawal or donation of electron density due to differences in electronegativity, impacting acidity, stability, and interactions with other molecules. Explore how inductive eff

2 views • 7 slides

Predicate calculus extends propositional calculus by introducing symbols like truth values, constants, variables, and functions. It allows for precise manipulation of components within assertions, enabling the creation of general statements about classes of entities. Learn how predicates define rela

5 views • 14 slides

Explore the world of deductive and inductive arguments through examples of deductive reasoning based on definitions and math, including categorical syllogisms, hypothetical syllogisms, and disjunctive syllogisms. Delve into inductive reasoning and the key distinctions between deductive and inductive

2 views • 26 slides

An in-depth exploration of the Material Theory of Induction applied to infinite lottery machines, discussing the challenges and strategies for making inductive inferences in such scenarios. The analysis covers probabilistic considerations, countable additivity issues, equal probability of outcomes,

3 views • 22 slides

Calculus plays a crucial role in solving optimization problems to find maximum or minimum values in various real-life scenarios. This content provides examples of optimizing for maximum profit, area, distance, and volume using calculus concepts. From finding optimal dimensions for fencing to maximiz

1 views • 10 slides

Join Lin McMullin in exploring the transition from the Mean Value Theorem (MVT) to the Fundamental Theorem of Calculus (FTC). Discover the significance of MVT, Fermat's Theorem, Rolle's Theorem, and the Mean Value Theorem, all crucial concepts in calculus. Engage in graphical explorations, proving m

1 views • 45 slides

Explore the connection between differential calculus and the definite integral through the fundamental theorem of calculus, which allows for the evaluation of complex summations. Discover the properties of definite integrals and how to apply the theorem to find areas under curves. Practice evaluatin

2 views • 15 slides

Explore advanced topics in vector calculus including gradient, divergence, curl, and theorems like the Divergence Theorem and Stokes' Theorem. Follow along with examples presented in Cartesian, spherical, and cylindrical coordinates to deepen your understanding of vector calculus concepts.

3 views • 29 slides

Delve into the realm of Programming by Example (PBE) and its motivating factors, distinctions from Programming by Demonstration (PBD), history of inductive learning, and the significance of generalization from observations. Explore how PBE and PBD fit into the landscape of inductive learning and mac

1 views • 32 slides

Machine learning models rely on inductive bias, which are the assumptions made by algorithms to generalize from training data to unseen instances. Occam's Razor is a common example of inductive bias, favoring simpler hypotheses over complex ones. This bias helps algorithms make predictions and handl

0 views • 20 slides

Explore the fundamental concepts of relational calculus and algebra in the domain of database management. Understand the differences between declarative and imperative query languages and learn to retrieve information using practical examples and theoretical frameworks such as tuple relational calcu

18 views • 23 slides

The global inductive power transfer system (IPT) market is evaluated $27.5 billion in 2024, is projected to expand at a CAGR of 26.1%, to reach $280.5 billion by 2034.\n\nRead Report Overview: \/\/bisresearch.com\/industry-report\/inductive-power-tra

3 views • 3 slides

Propositional calculus involves symbols representing true statements like "It is Monday" or "the car is red." Learn about connectives, semantics, and data-driven reasoning within this logical system. Predicate calculus expands on propositions by incorporating relationships between entities through p

4 views • 19 slides

Dive into essential strategies for conquering calculus anxiety, understanding derivative notation, and mastering key mathematical concepts. Explore practical tips and examples to enhance your skills and boost confidence in calculus. Overcome nervousness and confusion with expert guidance on function

2 views • 15 slides

This content provides information on Lecture 8 focusing on the calculus of variation, including topics like the Brachistochrone problem, calculus of variation with constraints, and its applications in classical mechanics. Questions from students are addressed regarding assignments, integral equation

1 views • 33 slides

This content delves into the methods of teaching mathematics, specifically focusing on the inductive-deductive method as explained by Dr. Meena Sharma. It elaborates on both inductive and deductive methods, highlighting their differences and applications in teaching math effectively. The content dis

2 views • 5 slides

In this workshop series, delve into the realm of fractional calculus at the MESA Lab, UC Merced. Gain insights on research interests, achievements, and current focus, along with near-term goals. Explore the significance of fractional calculus and its applications in Mechatronics, Embedded Systems, a

1 views • 5 slides

Explore the world of Stochastic Network Calculus in the Department of Electrical and Computer Engineering at Xidian University. Learn about Network Calculus, Queueing Theory, and the foundations laid by R. Cruz. Discover how Deterministic and Stochastic Network Calculus provide different levels of s

3 views • 43 slides

Explore the concepts of Big O notation, sorting algorithms, and inductive proofs in computer science. Learn about loop invariants, insertion sort, and the differences between weak and strong inductive proofs. Discover how to analyze algorithms for termination, correctness, time complexity, and memor

3 views • 43 slides

Explore the differences between inductive and deductive reasoning, where inductive involves making general statements from specific cases and deductive involves deriving specific instances from general statements. Learn how to identify and apply each type of reasoning through examples and explanatio

2 views • 13 slides

Discover the essential role of calculus in science and engineering education, emphasizing the significance of solid algebra preparation. Learn what it takes to excel in calculus and the background required for success. Gain insights from notable reports and examples to enhance your understanding and

3 views • 42 slides

Explore the concept of extrema and the First Derivative Test in Calculus through examples and explanations. Learn about absolute maxima and minima, local maxima and minima, and the importance of algebraic accuracy. Develop a comprehensive understanding of finding extreme values and applying derivati

4 views • 27 slides

Lambda calculus is a fundamental concept in functional programming, enabling the expression of functions and application of functions. Explore the syntax, examples, ambiguous parsing, disambiguation rules, and historical background of lambda calculus. Learn how lambda calculus has influenced modern

2 views • 56 slides

Explore how inductive thinking boosts higher-order mental processes, effective learning, collaboration, and problem-solving in educational settings. Discover the power of inductive models in generating higher levels of information acquisition and retention. Uncover strategies for enhancing students'

3 views • 13 slides

Learn about dental calculus, its composition, formation, and etiologic significance, along with predisposing factors and the primary cause of gingival inflammation being bacterial plaque. Explore the types and characteristics of calculus and its impact on oral health.

0 views • 30 slides

Delve into the concepts of concavity and the second derivative test in calculus, understanding critical numbers, local maxima and minima, intervals of concavity, and the relationship between these key calculus topics.

3 views • 40 slides

Explore various calculus topics including vertical motion, distance functions, integrals, the Fundamental Theorem of Calculus, and more. Delve into the core concepts of differential and integral calculus, and understand the inverse relationship between differentiation and integration. Discover the f

0 views • 21 slides

Explore various differentiation and evaluation problems in calculus, including straight line forms, chain rules, simplification, and more. Enhance your understanding of calculus concepts with these detailed examples and solutions.

0 views • 12 slides

The Fundamental Theorem of Calculus, Part 2, also known as the Evaluation Theorem, allows us to evaluate definite integrals by finding antiderivatives. This theorem connects differential calculus and definite integrals, providing a powerful tool in calculus. Learn how to apply this fundamental conce

4 views • 10 slides

Delve into the world of antiderivatives, differential equations, and slope fields in AP Calculus AB. Explore inverse operations, solving differential equations, and understanding antiderivatives as you deepen your calculus knowledge.

0 views • 15 slides

Learn about limits, derivatives, the product rule, the quotient rule, and the chain rule in calculus. Understand left limits, right limits, and how to compute simple limits, as well as the concept of continuity in functions. Discover why limits are essential in understanding the behavior of function

1 views • 41 slides

Discover detailed analysis and circuit conditioning guidelines for inductive sensor applications provided by Tim Green, MGTS Precision Op-Amp Applications Manager. Learn about a recommended circuit to scale customer inductive sensors into a 5V full-scale ADC input, ensuring minimal waveform distorti

9 views • 6 slides

Explore the foundational concepts of Lambda Calculus in Principles of Programming Languages at Arizona State University. Understand Function Application, Anonymous Functions, and more derived from Lambda Calculus.

1 views • 56 slides

Explore the concepts of limits, continuity, asymptotes, area problems, and tangent line problems in calculus using visual aids and explanations. Learn how limits behave as variables approach specific values and understand the relationship between functions and their behaviors near critical points. D

1 views • 36 slides

Explore the comprehensive approach to teaching Calculus at City College of San Francisco, including courses like Math 100A and Math 110A, as well as initiatives such as the AB1705 data-driven pilot program. Learn about the goals set for the STEM Calculus Pilot, the impact of the AB1705 calculus clau

3 views • 12 slides

Learn about Euler's Method, a recursive process used in calculus to approximate solutions to differential equations, and explore Logistic Growth models for population dynamics. Discover how these concepts are applied in real-world scenarios and improve your understanding of advanced calculus topics.

3 views • 6 slides

Explore innovative classroom techniques in teaching pre-calculus and trigonometry for better student understanding and success in calculus. Learn about the Mathematics Assistance and Learning Lab at UCF and the Emporium Model, emphasizing the importance of trigonometry for calculus preparation. Join

0 views • 14 slides

Explore the formal operational semantics of untyped lambda calculus within the context of programming languages. Discover how functions and local variables are defined, and learn about the fundamental concepts of Lambda calculus through examples and explanations provided by Dan Grossman in the CSEP5

4 views • 57 slides