Understanding Linear Congruences and the Euclidean Algorithm in Number Theory
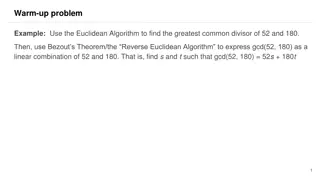
Exploring concepts of linear congruences using examples like finding times congruent to 2 o'clock and applying the Euclidean Algorithm to determine the greatest common divisor of 52 and 180. Learn about Bezout's Theorem for expressing GCD as a linear combination of the given numbers.
0 views • 26 slides
Recursive Algorithms in Computing
Explore recursive algorithms in computing, including the definition, examples like factorial, exponentiation, GCD, and modular exponentiation. Dive into the concept of solving problems by breaking them into smaller instances, ensuring termination with known solutions.
0 views • 16 slides
Understanding Linear Combinations and Common Divisors Theorem
Exploring the relationship between linear combinations and common divisors through the theorem connecting the greatest common divisor (GCD) and the smallest positive integer linear combination (SPC) of two integers a and b. The theorem states that the GCD is less than or equal to the SPC, with proof
0 views • 45 slides
Understanding Greatest Common Divisor and Euclidean Algorithm
Learn about the concept of greatest common divisors (GCD), how to compute them efficiently using the Euclidean Algorithm, the Quotient-Remainder Theorem, and the properties of common divisors. Explore examples and applications of GCD, extending to linear combinations, prime factorization, and other
0 views • 45 slides
Advanced Seminar on Problem Solving Techniques
Explore various problem-solving techniques such as prefix sum, hash, GCD, LCM, and more in this advanced seminar. Learn how to calculate complex mathematical functions efficiently and sort arrays in linear time complexity. Enhance your problem-solving skills and algorithmic thinking.
1 views • 23 slides
Understanding Cryptography: Basic Concepts in Number Theory and Divisibility
This text delves into the fundamental concepts of number theory, divisibility, and finite fields essential for understanding cryptography. It covers topics such as divisibility, properties of divisibility, the division algorithm, the Euclidean algorithm for determining the greatest common divisor, a
0 views • 35 slides
Understanding Euclid's Algorithm: An Ancient Approach to Finding Greatest Common Divisors
Euclid's Algorithm, dating back 2500 years, offers a simpler method to find the greatest common divisor (gcd) of two non-negative integers compared to traditional factorization. By iteratively applying a rule based on the gcd of remainders, it efficiently computes gcd values. The basis of the algori
0 views • 15 slides
Basic Concepts in Number Theory and Finite Fields for Cryptography
In this presentation, the basic concepts of number theory, including divisors, properties of divisibility, the division algorithm, and the greatest common divisor (GCD), are explored in the context of cryptography and network security. The importance of finite fields in cryptographic operations such
0 views • 38 slides