ADFGVX Cipher: Encryption and Decryption Techniques
Discover the ADFGVX cipher, a historical encryption method used to secure messages during World War I. Learn about Fritz Nebel and Gino Painvin, who played significant roles in its development. Explore the Polybius Square invented by Polybius in the 2nd century BC for converting letters to numbers. Understand the processes of substitution and transposition in ADFGVX encryption, along with decryption methods. Dive into encryption strategies, such as key transposition using the RIFLE method, and explore practical examples of encrypting and decrypting messages with the ADFGVX cipher.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
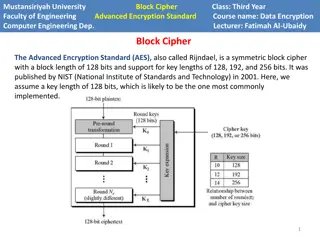
Content ADFGVX
ADFGVX Fritz Nebel 1891-1967 ADFGX Painvin 1886-1980 1918
ADFGVX Polybius Square: Invented by Polybius( 2th BC) To convert letters to numbers e.g., h would be 23.
ADFGVX : Substitution + Transposition AX AV XX GX FG VX AG XX AA AV FG AF FF XX AV GX AX XA XV I love problem solving Figure: Substitution process
ADFGVX Transposition: Key: RIFLE R I F L E E F I L R 5 3 2 4 1 1 2 3 4 5 AX AV XX GX FG VX AG XX AA AV FG AF FF XX AV GX AX XA XV XGXVFVXF AXAAAXAV XGXAGXXX VFGAFAXG AXVXFFGA A X A V X X A X V A In in rows X G X F G G X G F X rearrange Out in columns V X A G X X A X G V X A A A V V A A A X F G A F F F A G F F F X X A V V X X A F G X A X X X A X X G A X V G F F V X G A
ADFGVX ?, Key ? Substitution: ?:A ? ? such that ? is a bijection. Transposition: (Append ?(? to let |?(? | be a multiple of |?| ?(? [?] (? ??? |?|,? mod |?| (? ??? |?|,?(? mod ? ?[(|?(? | ??? |?| ? ? mod ? Where ? ?? ? reverse permutation for the order of the character in ? ? A = {A,B,...,Z,0,1,...,9 ? = {?,?,?,?,?,? ? ?(? + ? ??? |?|
Encrypt_ADFGVX(?,?,?) Let ?,? be a new string For ? = 0 to ?.length 1 ? 2?,2? + 1 = ?(?[?] Append ? to let ?.length be a multiple of ?.length Calculate ? from ? n = ?.length,m = ?.length For ? = 0 to ?.length 1 ? (n ??? m ? ? mod ? + ? ??? m = ?[?] return ?
Decrypt_ADFGVX(?,?,?) Let ?,? be a new string n = ?.length div W.length , m = W.length Calculate ? 1from ? For ? = 0 to ?.length 1 ? ? ??? ? ? + ? 1(? ??? n = ?[?] Calculate ? 1 from ? Shrink ? to let ?.length be a multiple of 2 For ? = 0 to ?.length 1 ???? = 2 ? ? ??? 2 =? 1(? ? ,? ? + 1 return ?
Assume that large amount of encrypted text is intercepted Substitution: A D F G V X A ?1 ?7 ... ?13 ?19 ?25 ?31 ?2 ?3 ?4 ?5 ?6 ? =Sort(?) ? =Sort(?) ? [i] D F ? ? G ? [i] V Frequency in encrypted text X ?36 A B C Z 0 1 2 9 ?1 ?2 ?3 ?26 ?27 ?28 ?29 ?36 Frequency in Statistics
Transposition: :Consider two texts with a few words identical from the beginning E F I L R 1 2 3 4 5 I love problem solving (left with 300 words) X A X V A Find identical pattern in both texts for the following text, partition the text by the same pattern into column-first table. G X G F X X A X G V V A A A X I love problem solving for 999 times (left with 999 different words) F A G F F The column with length k+1 has higher rank. The column with length k has lower rank. If the column is short in both two text, then properly with the lowest rank. If both k+1, then properly the highest rank. V X X A F X A X X G V X A