Understanding Torque in Mechanics
Explore the concept of torque in mechanics, which is a twisting force that can cause angular acceleration. Learn how to calculate torque by multiplying the distance from the rotation center and the applied force, and understand the importance of the angle between force and distance. Discover practical examples and calculations involving torque in various scenarios to deepen your understanding of this critical concept in physics.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
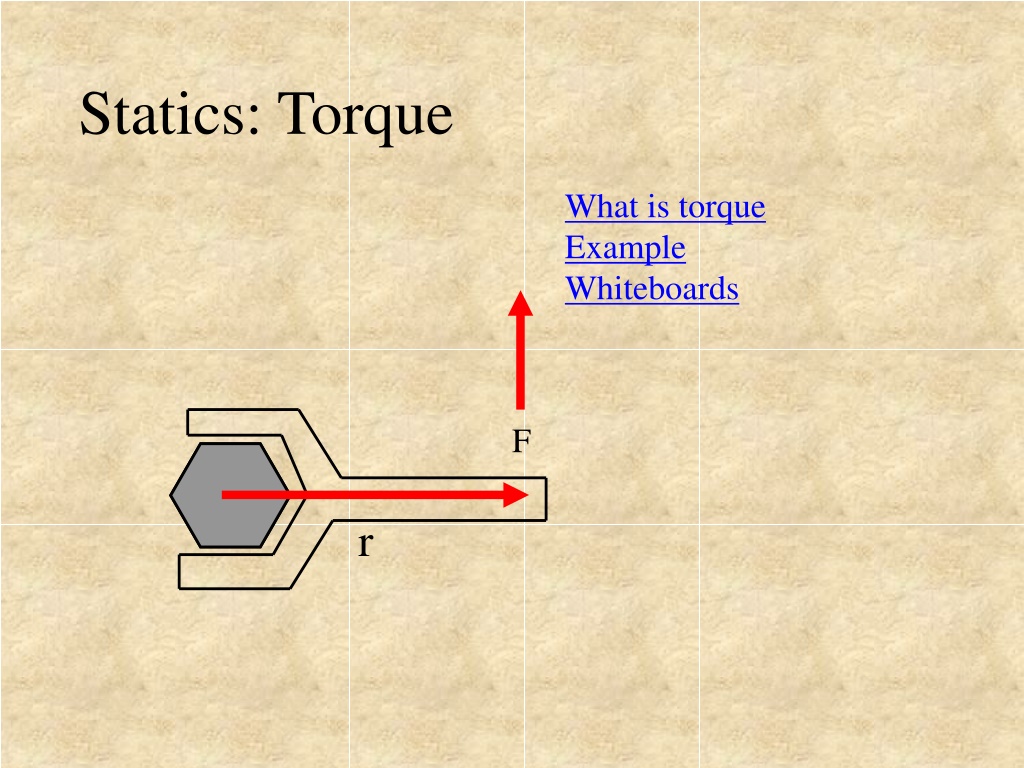
Statics: Torque What is torque Example Whiteboards F r
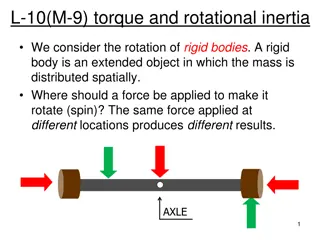
Angular Mechanics - Torque TorqueA twisting force So how do you increase torque? Push farther out: or F F Push with more force: TOC
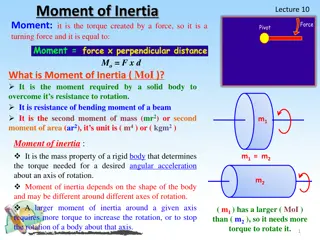
Angular Mechanics - Torque TorqueA twisting force that can cause an angular acceleration. = rxF F r If r = .5 m, and F = 80 N, then = (.5m)(80N) = 40 mN. Torque is also in foot pounds (Torque Wrenches) TOC
Angular Mechanics - Torque TorqueA twisting force that can cause an angular acceleration. = rxF = rFsin F Fsin r Only the perpendicular component gives rise to torque. (That s why it s sin ) TOC
Tough Example:Whats the torque here? = 56o F = 16 N r = 24 cm Ok This is as tricky as it can be: use = rFsin , r = .24 m, F = 16 N But use not 56o. You want to use the angle between r and F which is 90 56 = 34o Finally, = (.24 m)(16 N)sin(34o) = 2.1 mN TOC
Whiteboards: Torque 1 | 2 | 3 TOC
What is the torque when you have 25 N of force perpendicular 75 cm from the center of rotation? = rFsin = (.75 m)(25 N) sin(90o) = 18.75 mN = 19 mN W 19 mN
If you want 52.0 mN of torque, what force must you exert at an angle of 65.0o to the end of a .340 m long wrench? F 65o .340 m = rFsin 52 mN = (.34 m)(F) sin(65o) F =(52mN)/((.34m) sin(65o))=168.75 N F = 169 N W 169 N
The axle nut of a Volkswagen requires 200. foot pounds to loosen. How far out (in feet) do you stand on the horizontal wrench if you weigh 145 lbs? = rFsin 200. ft lbs = (r)(145 lbs) sin(90o) r = (200. ft lbs)/(145 lbs) = 1.3793 feet r = 1.38 feet (1 41/2 ) W 1.38 feet