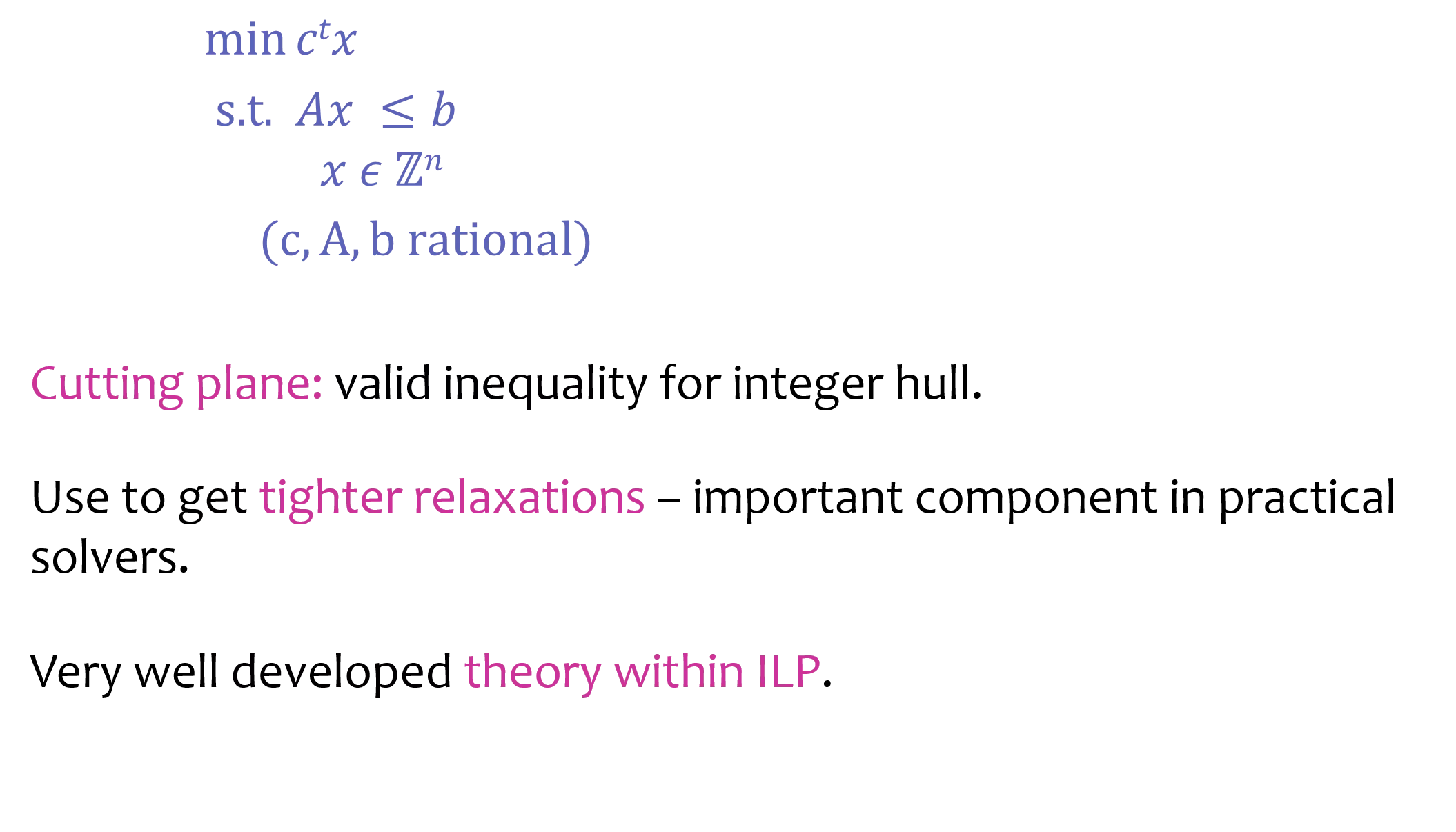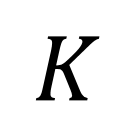Advances in Integer Linear Programming and Closure Techniques
Explore cutting planes, convex integer programming, Chvátal-Gomory cuts, and closure methods in nonlinear integer programming. Discover how these techniques enhance the efficiency and effectiveness of integer programming models, leading to substantial progress and improved solutions.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Elementary Closures in Nonlinear Integer Programming Daniel Dadush CWI Santanu Dey Georgia Tech Juan Pablo Vielma MIT
Cutting Planes for Integer Linear Programs min??? s.t. ?? ? ? ? ? (c,A,b rational) ? Cutting plane: valid inequality for integer hull. Use to get tighter relaxations important component in practical solvers. Very well developed theory within ILP..
Mixed and Non Linear Models? min? ?,? s.t. ??(?,?) 0 ? ? ? ?,? ? ? ? Many other important Integer Programming models. Substantial Progress in recent years: Solvers, Complexity, Heuristics, etc. Cutting planes poorly understood, even when objective and constraints are convex.
Convex Integer Programming min? ? s.t. ??? 0 ? ? ? ? (?,?? ? ? ??????) Goal: understand basic behavior for fundamental classes of cutting planes. Issue: most current theory depends heavily on rational linear structure. Plan: Develop stronger / more robust Analytical Tools.
Chvtal-Gomory (CG) Cuts ? ?compact convex ? ? Support function of ?: ??? = max? ? ??,? ? ? For ? ? ?,CG cut: CG ?,? = {?: ?,? ??? }
Chvtal-Gomory Closure ? ?compact convex ?1 CG closure of ?: ?6 CG ? = CG(?,?) ? ?2 ? ? ? ?3 ?5 ?4
Chvtal-Gomory Closure ? ?compact convex ?1 CG closure of ?: ?6 CG ? = CG(?,?) ? ?2 ? ? ? ?3 ?5 ?4
Chvtal-Gomory Closure ? ?compact convex ?1 CG closure of ?: ?6 CG ? = CG(?,?) CG(?) ?2 ? ? ? Chv tal `73: Converge to integer hull after finitely many iterations. ?3 ?5 ?4
Split Cuts ? ?compact convex Elementary disjunction: ? ? ? ? ?? ? ? ? + 1 ? ? ?,? ?
Split Cuts ? ?compact convex Elementary disjunction: ? ? ? ? ?? ? ? ? + 1 ? ? ?,? ? Split Cut: SC ?,?,? = conv(? ? ? ? ? ? ? ? + 1 )
Split Closure ? ?compact convex Split Closure: SC ? = SC(?,?,?) ? ?? ?,??
Split Closure ? ?compact convex Split Closure: CG(?) SC ? = SC(?,?,?) ?? ?,??
Split Closure ? ?compact convex Split Closure: SC(?) SC ? = SC(?,?,?) ?? ?,??
Generating the CG Closure Schrijver 1980 Theorem: If ? = {? ?:?? ?}is a rational polyhedron, then CG(?) is finitely generated. ?1 CG ? = CG(?,?) ?4 ? ? ? ? ?2 ?3
Generating the CG Closure Schrijver 1980 Theorem: If ? = {? ?:?? ?}is a rational polyhedron, then CG(?) is finitely generated. ?1 CG ? = CG(?,?) ?4 ? ? ? CG(?) ?2 ?3
Generating the CG Closure Schrijver 1980 Theorem: If ? = {? ?:?? ?}is a rational polyhedron, then CG(?) is finitely generated. ?1 Question: Is this true in general? ?4 CG(?) ?2 ?3
Generating the CG Closure Schrijver 1980 Theorem: If ? = {? ?:?? ?}is a rational polyhedron, then CG(?) is finitely generated. Question: Is this true in general? Not always. 2?1 ?2 .1 ?2 0
Generating the Split Closure Cook, Kannan, Schrijver 1990 Theorem: If ? = {? ?:?? ?}is a rational polyhedron, then SC(?) is finitely generated. ?1 SC ? = SC(?,?,?) ?4 ?? ?, ?? ? ?2 ?3
Generating the Split Closure Cook, Kannan, Schrijver 1990 Theorem: If ? = {? ?:?? ?}is a rational polyhedron, then SC(?) is finitely generated. ?1 SC ? = SC(?,?,?) ?4 ?? ?, ?? SC(?) ?2 ?3
Generating the Split Closure Cook, Kannan, Schrijver 1990 Theorem: If ? = {? ?:?? ?}is a rational polyhedron, then SC(?) is finitely generated. ?1 Question: ?4 SC(?) Is the Split Closure always polyhedral? ?2 ?3 No.
Non Polyhedral Split Closure D., Dey, Vielma 11 Theorem: The split closure of an ellipsoid can be non polyhedral.
Generating the CG Closure D., Dey, Vielma 11 Theorem: If ? ?is compact convex, then CG(?) is proper and finitely generated. ?1 CG ? = CG(?,?) ? ? ? ?4 ? ?2 ?3
Generating the Split Closure D., Dey, Vielma 11 Theorem: If ? ?is compact strictly convex, then SC(?) is proper and finitely generated. ?1 SC ? = SC(?,?,?) ?? ?, ?? ?4 ? ? is strictly convex if ?? does not contain lines. ?2 ?3
Generating the CG Closure D., Dey, Vielma 13 Theorem: If ? ?is a thin, totally closed convex set with rational polyhedral ???(?), then CG ? is proper and finitely generated. ?1 CG ? = CG(?,?) ? ? ? ?4 ? If ? is closed convex with CG ? proper, non-empty & rational polyhedral then: 1. ? is thin. 2. ???(?) is rational polyhedral. ?3
Thin Convex Sets Definition: Closed convex set ? is thin if ? ??? ? + ??2 for some finite radius ? 0. ? Thin Not Thin
Thin Convex Sets Definition: Closed convex set ? is thin if ? ??? ? + ??2 for some finite radius ? 0. ? Lemma: If ???(?) is polyhedral, then ? is thin for generators cone ?1, ,?? =rec ? , max i [?] max ? ? for some constant M 0. ?,? ?
Totally Closed Sets Definition: A convex set ? ?is totally closed if ProjW(?) is closed for any subspace ? of ?. Not Totally Closed Totally Closed
Totally Closed Sets Definition: A convex set ? ?is totally closed if ProjW(?) is closed for any subspace ? of ?. Thin & Totally Closed
Totally Closed Sets Definition: A convex set ? ?is totally closed if ProjW(?) is closed for any subspace ? of ?. Lemma: If ???(?) is polyhedral, then ? is totally closed for every face ? of ??? ? , the projection of ? onto span(F) is closed.
Building the CG Closure ? ? denotes the partial closure. 1. Achieve Containment: CG ?,? ? ? Most difficult step (trivial for rational polytopes). Need tools from Convex Analysis and Geometry of Numbers.
Building the CG Closure ? ? denotes the partial closure. ?? ?,? ?? 1. Achieve Containment: CG ?,? ? ? 2. Complete the Boundary: CG ?,? ?? ?? ? ?? Only a finite number of faces of ? need fixing. Use induction on each face.
Building the CG Closure ? ? denotes the partial closure. 1. Achieve Containment: CG ?,? ? ? ? ? 2. Complete the Boundary: CG ?,? ?? ?? ? ?? ? ? ? 3. Complete the Closure: Add all cuts separating a vertex of CG(?,?). All remaining cuts have bounded norm.
Lifting CG cuts D., Dey, Vielma 11 Theorem: Let ? be an exposed face of ?. Then CG ? = CG ? ?. ? ? Goal: Lift CG(?,?) to ?. ? ? ? Find ? : CG(?,?) = CG(?,? ) 1. on rational part of ?. 2. Remove irrational parts of ? using additional CG cuts. ?? ?
Removing Irrational Parts Since ? is an irrational line segment, a rational polytope contained in ? can only intersect ? at 0. Need CG cuts that remove irrational parts of ?. (3 2,2 3) Rational Polytope 0 ? ? ?
Removing Irrational Parts Kronecker s Approximation Theorem Fractional part is dense. (3 2,2 3) 0 ? ? ?
Removing Irrational Parts 3 2 Integers close to ( nearly same inequality for K. 3) line give 2, (3 2,2 3) 0 ? ? ?
Removing Irrational Parts Use density to find close cuts biased towards opposite sides of ?. Cuts remove irrational parts of ?. (3 2,2 3) 0 ? ? ?
Extending to General Convex Sets Main Technical Issues: 1. Can only build CG cuts in integer directions where the objective value is finite. (need thinness and rational polyhedral recession cone) 2. To lift CG cuts from faces must show fine continuity properties of the objective function. (need total closedness)
Open Question Is the split closure of a compact convex set finitely generated?